2.1 Gamma 图表的基本术语
皮尔斯在做出以上断定平面的集成设想之后,便着手构建EGs 的第三类图表系统。这个图表系统用一种丰富早期指号系统的方式,首先给出的术语是关于割线的。我们以“天正在下雨”这个语句的图表为例,来说明皮尔斯给出的这个关于割线的新术语。
如果有一个指号“天正在下雨”被我们断定,这在Beta 图表中只是在一个断定平面上。如果我们构建了第三种图表系统Gamma 图表系统,那么我们对这个语句的理解,依据皮尔斯的分析,这样一个新图表中的语句,则很可能有进一步的意义。
这个图表并不断定天不下雨,它仅仅断定:Alpha 图表和Beta 图表的规则并未逼迫我去承认天下雨;或者仅仅断定:达到同样结果的某种东西,即一个人,他除了精通于体现在EGs 中Alpha 图表和Beta 图表的逻辑之外,对其他一概无知,他将不知道天下过雨。[5]
这段原文既难翻译也难理解,这里也许涉及皮尔斯对话语图表的博弈思想,即图表的绘制者和图表的解释者双方的博弈。当我绘制出一个图表时,绘制图表的人会有一个意义。但图表是给人看的,看这个图表的人会对图表做出解释,这被称为解释者,解释者也会有一个意义。[6]那个精通前两个图表所体现的逻辑的人,除此之外一无所知,他看到图表就会对图表有一个理解,这可以看作是解释者。既然他精通于两个图表所体现的逻辑,其他一概不知,他当然也不知道天正在下雨。因此断定他不知道天下过雨,也是可以理解的。皮尔斯这段引文所要说明的,就是Gamma 图表系统的第一个术语:折断割线(broken cut),在图表上就描述为由折断割线环绕的一个封闭圈。上述引文中的“天正在下雨”在Gamma 图表系统中作如是理解,就是因为这个语句被折断割线所包围,成为一个模态语句。
折断割线
由此,我们把折断割线定义为这样一种意义上的术语,设折断割线环绕的语句为A,则折断割线的含义可以理解为:并不迫使解释者承认在其内的语句A 是真的。把这个含义再转换为带模态的解释,那就是,折断割线表示:
并非A 是可能的。
因此折断割线仍然保持了它在另两个图表系统中的否定的含义。
依据折断割线的这一定义,可以给出以下模态语句的Gamma图表。
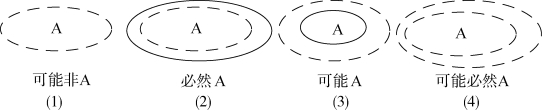
图表13 使用折断割线表述模态语句的Gamma 图表
潜在和选择
在Beta 图表中,我们在空位中能够填入的节点是普通个体或者个体类。依据皮尔斯的构想,在Gamma 图表中,这些节点的填充则和潜在类别相关。这里的潜在类别应该理解为非实在的类别,由这些非实在类别中选择的语词,自然也是非实在的。那么什么称作潜在(potentials)?什么称作在潜在类别中的选择(selectives)呢?皮尔斯给出了以下的描述。
置于潜在存放处(the left of potentials)的选择是一个奇怪类别的专有名词,因为它并不指称普通个体,而是指称品质上的可能性,这种品质上的可能性并没有个体特性。[7]
潜在和选择被看作是Gamma 图表的两个新观念,在Gamma图表中,我们不仅要处理Beta 图表里面的实在个体,还要处理超实在的潜在。这些超实在的潜在实质上就是抽象。因此,我们在Gamma 图表中讨论的对象是抽象的对象,图表中的节点和述位,应对的是我们语言中的抽象概念。
由此,我们可以把潜在看作是包含那些表述可能性的节点,它处在一个和其他指号类别,图表的指号以及图表元素完全不同的基础之上。而选择则属于潜在,但属于我们在潜在中挑选出来的某个可能性,例如上述引文中非实在的专有名词。我们先给出Gamma 图表表达潜在的几个图例,然后继续说明选择。
设我们有以下几类表达抽象潜在的命题形式,下面横杠表示空位。
(1)____是一个命题/图表。
(2)____有一种____品质。
(3)____位于____和____之间的二元关系之中。
(4)____位于____,____和____之间的三元关系之中。
对于这4 个命题形式,可以使用Gamma 图表表述为以下图表14 中的相应子图表。
由此,本章1.1 中的语句(1):“亚里士多德具有所有哲学家的优点”就可以用Gamma 图表来表述为图表15。
我们再对选择概念做一些说明,因为这个概念是贯穿于EGs之中的,我摘录泽曼的一段话来完成这个任务。在皮尔斯图表一文中,泽曼说:
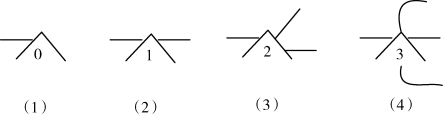 (https://www.daowen.com)
(https://www.daowen.com)
图表14 抽象潜在的Gamma 图表
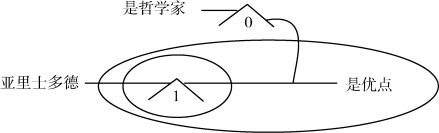
图表15 本章1.1 中语句(1)的Gamma 图表
在我进入涉及图表的任意技术性问题之前,我愿意简单地回答我在前面提及到的问题:为什么皮尔斯,他已经在1880年就建立起一个成功的代数逻辑,却还要花费很大的心力再去构建EG 呢?皮尔斯本人回答了这个问题。在EG 的构思中,皮尔斯有等同线的术语,但他又引入了一个和等同线有同等意义的变体性概念;在论域中的对象可以用它称之为选择(selectives)的东西来表述,这也正是有区别的等同线所表述的。在代数中,选择更像一个常规性的变元,虽然也像那个等同线,它的量词是隐含的。[8]
然后,泽曼给出一个代数式和一个图表式的语句形式,来说明上面提及到的选择概念。
对于命题形式“X 是红的”和“X 是圆的”,我们也可以用等同线的方式来表述它们,这可以表述为以下图表16,这里的选择类似于我们在等同线的共存在端点填入某个对象,对Gamma图表而言就是那个古怪的专有名词。按照皮尔斯的说法就是:
至少,这个意见是十分肯定的,等同是一种简单的关系。但是,在以下图表(指下面的图表16)中,替代选择的等同线,非常明确地表述了等同属于普遍连续性和属于特指线形连续性。[9]
这段引文中,皮尔斯是在Alpha 图表和Beta 图表中讨论等同,它当然是简单的。但Gamma 图表中的等同显然复杂很多,因为那里的等同不仅涉及个体的实在,还涉及可能个体的出现,因此选择被看作是一种关系,一个语义学的术语。
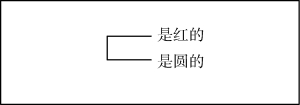
图表16 替代选择的命题形式等同线表述
关于选择这一术语,我们就简单讨论到这里。在皮尔斯对于Gamma 图表具有以上设想的术语之后,过了几年,皮尔斯思考下述语句的图表表述。
“存在一个女人,她不是并且不可能等同于任何可能的天主教徒。”
他发现,这是一种关于不可能性的描述,也许美国当时的女性没有信仰天主教的权利。于是,皮尔斯设想了一种阴影方式的图表来表述这样一个语句。
折断割线阴影中的天主教徒,表述天主教徒的存在是被否定的,该图外的女人则意味着存在。(见图表16)皮尔斯设想的这样一种对于不可能的表述方式,导致了产生Gamma 图表中另一个重要术语:色标(tinctured)。
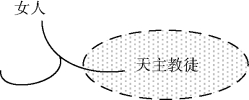
图表17 不可能语句的Gamma 图表
色标
色标是Gamma 图表特有的术语,皮尔斯扩展了折断割线的概念,他让断定平面SA 的页面颜色各不相同,无色彩的页面表示实在世界的断定平面,有色彩的断定页面则可以表示各种各样的可能性,如同以下图表18 所示。
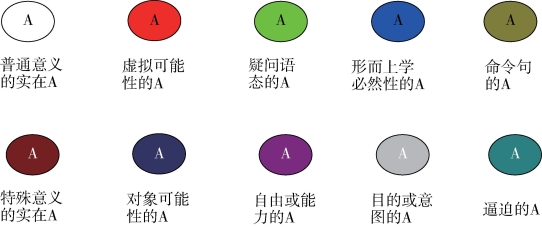
图表18 表示各种实在和非实在可能性的色标图[10]
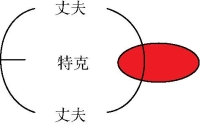
图表19 虚拟可能性命题的色标图
皮尔斯用这种色标的图表,来说明他列举的一个语句的Gamma 图表,这个语句是:“存在特克(Turk)这个人,他是两个不同人的丈夫。”
当时美国的婚姻法当然不可能存在这种情况,所以它是一种虚拟的可能性,这可以用图表19 表述。
由这个色标概念,自然可以设想如何描述真势模态逻辑,也可以设想如何描述认知逻辑、道义逻辑、信念愿望意图的逻辑和祈使句的逻辑等。但看得出来,实际上的运用,还有待很多复杂问题的解决。
