3.2 信息状态、选择和可通达关系
在描述Gamma 图表的时候,我们就已经指出过,选择是一种关系(见本章2.1)。现在我们有了皮尔斯的“信息状态”术语,就可以较为方便地讨论“选择”了。
Gamma 图表引入折断割线来表述模态命题,引入折断割线所造成的困惑是,因为折断割线封闭的图表所表达的命题,它总是和多种信息状态相关,仅用折断割线无法分别不同的信息状态。于是,我们就有了“选择”概念,在本章2.1 中,我们已经指出等同的含义:
替代选择的等同线,非常明确地表述了等同属于普遍连续性和属于特指线形连续性。[20]
而这段引文把等同看作是对选择的替代,选择自然也是一种关系。但这里选择所代表的关系则和关系的主体紧密相联,它是把关系和关系项一并来考虑的。把信息状态概念放进来,选择所表示的关系,很容易理解为是信息状态和信息状态之间的某种关系。选择的意义恰在于除了有关系的意义之外,还有对关系主体予以选择的意义。以下一段皮尔斯的论文摘录,较为清晰地表述出来,皮尔斯所讲的选择,实际上类似于可能世界语义学的可通达关系。皮尔斯在评论某些人对Gamma 图表的理解时,有这样一段说明:
所以,你理解:在处理折断割线当中,如果我们不给折断割线附加上一个指号以区分它所指称的特殊信息状态,我们将陷入无可避免的混淆。随之,一个类似的指号必定加进那个简单指号G,G 提及到那个信息状态,即在知道该图表为真的那个时间之中的信息状态。因为这个目的,我使用以下交叉线标志,所以有:这些选择在提及到信息状态当中,是非常特殊的,似乎它们是个体状态。除此之外,这些选择还有一种附加的特性,它们是有限的连续序。[21]
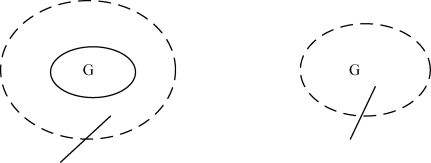
图表25 交叉线标志图
实际上,借助于这个等同线交叉标志,也就是选择,图中G的信息状态就和图外的信息状态连通起来,它所起的作用非常类似于可通达关系。(https://www.daowen.com)
皮尔斯还给出一个认知逻辑的实例,虽然在他那个时代还没有想象到认知概念也可以构成模态逻辑。
如果我们有一个可构想的信息状态,在这个信息状态中,知道者知道图表G 为真,并且他还不知道另一个图表H 将是真的,那么,我们如何用图表来表示这样的信息呢?皮尔斯给出了以下的图表26。
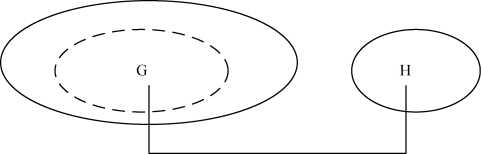
图表26 不同信息状态的Gamma 图表
图表26 中,G 所在图是一个信息状态,H 所在图是另一个信息状态,通过等同线把这两个信息状态连接起来,其中的一个信息是被断定的,另一个信息则是不知可否的。后来,皮尔斯进而设想了一个更为简洁的表述信息状态图表的形式,用一个带箭头的连线来连接两个语句,表示一个信息状态下的语句A和另一个信息状态下的语句B 之间,从B 到A 的可通达关系。
![]()
图表27 信息状态语句的简化Gamma 图表
