2.3 用Gamma 图表表述模态系统S5
皮尔斯的Gamma 图表虽然不完善,但已经具有基本的模态系统构想,本节我们使用Gamma 图表来表述模态系统S5。尽管这种Gamma 图表已经在皮尔斯基础上有所完善,但基本框架仍然是皮尔斯Gamma 图表的,所以称作用Gamma 图表表述模态系统S5。[16]因为用图表方式来表达一个模态系统异常复杂,我们在给出基本术语和规则之后,仅用一个模态S5 图表推演的实例来说明S5 的Gamma 图表系统。
2.3.1 基本图表术语
我们在Alpha 图表系统中已经给出一些基本的图表术语,但要在Alpha 图表基础上构建S5,还需要一些相关的术语和图表规则。我们先给出相关术语,再给出相应构图规则。
S5 的Gamma 图表至少需要以下基本术语,我们才能说明它的基本规则和图表推演。
图表的单一出现
给定图表A 和B,并且给定命题符号p,其中p 在图表A 中仅只出现一次。我们再给定表达式A [B] 指称这样的图表A,其中图表B 中的公式已经被替换为p 的出现。这种符号将用来指出,在一个封闭图表中的某个图表的单一出现。图表的单一出现术语表达了S5 的Gamma 图表假定了一个命题公式和一个图表在不至于混淆的情况下,它们表达同样的东西。
否定语境、肯定封闭和否定封闭
假定我们有图表¬(A),则图表¬(A)去掉A 的那一部分¬(…)称作否定语境。
一个图表在A [B] 中是肯定封闭的,当且仅当,它在偶数个否定语境中出现。
一个图表在A [B] 中是否定封闭的,当且仅当,它在奇数个否定语境中出现。
模态语境和模态封闭
假定我们有图表□(A),则图表□(A)去掉A 的那一部分□(…)称作模态语境。
如果一个图表它在一个模态语境中出现,则这个图表就是模态封闭的。
图表导出
一个图表系列A1,A2…An,构成了一个从A1 到An 的图表导出,当且仅当,每一个图表Ai+1,可以从Ai 通过运用以下图表规则来获得。
2.3.2 基本规则
(R1)插入规则
任意图表都可以绘制在处于否定封闭图表中的任意地方。
(R2)消去规则
任意肯定封闭图表可以消去。
(R3)重置规则
任意图表A 的复本可以绘制在不是处于图表A 之中的任意地方,假定仅有通过的语境是否定语境,这些否定的语境并没有封闭A。
(R4)拆置规则
任意图表,只要这些图表能够看作是运用重置规则获得的结果,它们就可以被消去。
(R5)双重否定规则(https://www.daowen.com)
一个双重否定语境可以绘制在任意图表周围,同时,任意图表周围的双重否定语境也可以被消去。
以上规则是关于Alpha 图表的导出规则,加上以下规则就成为处理模态逻辑的Gamma 图表系统了。
(R6)否定□引入
一个模态语境可以在任意否定封闭图表周围绘制。
(R7)肯定□引入
一个模态语境可以在任意肯定封闭图表B 周围绘制,B 不是模态封闭的,但假定了在某个语境之内封闭了B,又不在B 之内的每一个命题字母是模态封闭的。
(R8)□左规则
如果Γ,A├C,那么,Γ,□A├C。
(R9)□右规则
如果Γ├A,C,那么,Γ├□A,C,假定在Γ 或者A 中出现的任意命题字母是模态封闭的。
(R10)肯定□消去
在任意肯定封闭图表周围的模态语境是可以消去的。
2.3.3 S5 定理和公理的图表推演
运用Alpha 图表的导出规则,我们可以给出一个命题逻辑的推演图示,以下图表22 是Alpha 图表的一个推演。
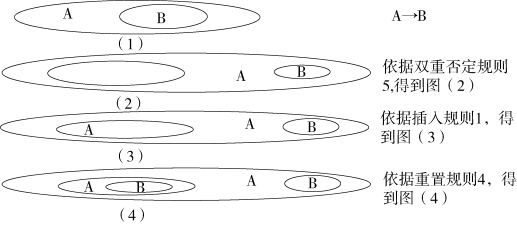
图表22 Alpha 图表的一个推演
显然,这个图表22 不过是在图中重复了A→B,但这个重复可以导出K 的分配公理。这可以用图表23 来表述,图表23 中的图(5)是依据规则6 从图表22 中的图(4)获得的。
而图表23 中的图(7),恰好就是K 系统中的分配公理□(A→B)→(□A→□B)。
几乎是使用同样的有关必然的规则,我们可以从一个重言式A→A 出发来获得S5 的公理:◇A→□◇A,这可以用图表24来表述。
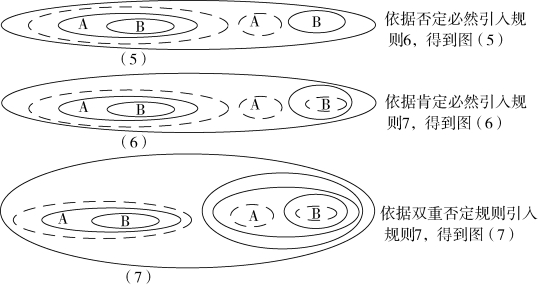
图表23 K 分配公理的证明图
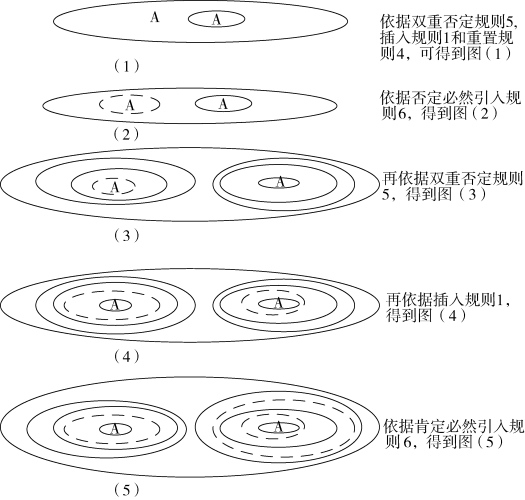
图表24 S5 公理(◇A→□◇A)证明图
这个S5 推演图表的最后图(5),就是S5 公理(◇A →□◇A)。
