2.2 Gamma 图表的若干规则
从以上给出的EG 术语,我们可以看到,在表达模态的Gamma 图表中,最重要的图表新元素是折断割线和色标,这些新元素可以用来表述各种各样的模态。限于Gamma 图表色标的复杂性,关于色标的表述方式仍然是不成熟的,因而整个Gamma 图表也是不成熟的。皮尔斯在他1906年的论文中,提到这个Gamma 图表时,也把它看作是一个不成熟的系统。
但是,Gamma 图表仍处在幼儿阶段。还将需要许多年的时间,后面的人才能够把这个图表系统,达到Alpha 图表和Beta 图表现在已经达到的完美程度。[11]
这很明显,因为皮尔斯所能做到的,也仅仅是单一色标表达的单一模态。皮尔斯在上述同一篇论文中,仅为这种单模态逻辑提供了若干规则,即使是单模态的这些规则也是不完善的,需要我们继续的修改和补充,皮尔斯称这些规则为允许(permissions)。[12]
皮尔斯首先给出的是两个对偶性的规则,一对是消去(Deletion)和插入(Insertion)规则,我们称之为规则(1);另一对是重置(Iteration)和拆置(Deiteration)规则,我们称之为规则(2)。
消去(Deletion)和插入(Insertion)规则:任意图表特例都可以从任意的页面(recto)区域(包括任意等同线的所指)中被消去,任意图表特例可以在任意页面(verso)区域(包括作为图表特例的任意两条等同线的并列或者三等同点的并列)中被插入。
重置(Iteration)和拆置(Deiteration)规则:在任意区域描述的任意图表,可以从那个区域或者从包括在其内的任意区域重置或者可以依据消去规则拆置(如果已经被重置的话)。这涉及随意让等同线变形的规则。[13]
在皮尔斯1906年论文中,他继续给出另外两条规则,双重割线规则(3)和最小割线规则(4)。
双重割线规则:两条割线互为表里,其间不含任何东西,除非它是从外部割线之外到内部割线之内的连字符,这样的两条割线可以在任意区域形成和取消。
第四条允许:如果最小的割线,它整个含有一个连接不同领域中两个图表的连字符,这样的割线在相对于含有那两个图表的最小割线区域页面的那一边上有其区域,那么,这类连字符可以随心所欲地做成或者中断,只要这两个图表涉及。[14]
应用这四条规则中的前两个规则,我们就可以表示以下语句,并用这类语句进行推理。如果我们有语句:存在一个女人,每一个天主教徒都喜欢她,那么,以这个语句为前提,我们就可以依据重置规则(2)将等同线变形为下左图,然后运用消去规则(1)导出如下语句:每一个天主教徒必定喜欢某个女人,即图表20 下右图。
应用这两个规则再加上第三个规则,我们还可以给出一个模态三段论的推理。(https://www.daowen.com)
设有如下模态三段论:
任何人必定是动物,(1)
任何动物必定是有死的,(2)
所以,任何人必定是有死的。(3)
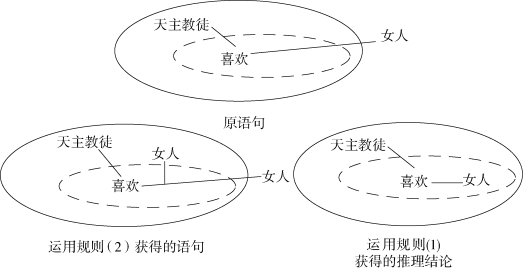
图表20 Gamma 图表规则(1)(2)应用图
这个推理可以表述为以下Gamma 图表21。[15]
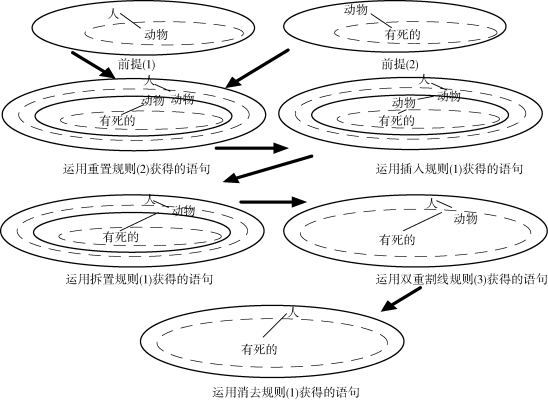
图表21 模态三段论推理的Gamma 图表
皮尔斯关于Gamma 图表的规则,例如规则(3)是有问题的,规则(4)更令人怀疑,我们不在此赘述,有兴趣的读者可参看本章所引用的参考文献全文。有关Gamma 图表规则的论述,先暂且到此。
