2.1　离散分布

2.1　离散分布

有些随机变量全部可能取到的值是有限个或可列无限多个,这种随机变量称为离散型随机变量。例如,某城市的120急救电话台一昼夜收到的呼唤次数就是离散型随机变量,而如果用T记灯泡的使用寿命,T的可能取值充满一个区间,是无法按一定次序一一列举的,所以灯泡的使用寿命T是一个非离散型随机变量。

要掌握一个离散型X的统计规律,必须且只需知道X的所有可能取值以及取每一个可能取值的概率。设离散型随机变量X所有可能取的值为x k(k=1,2,…),X取各个值的概率,即事件{X=x k}的概率为

P{X=x k}=p k,k=1,2,…

由概率的定义,p k满足如下两个条件:

①p k≥0,k=1,2,…;

②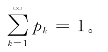

我们称P{X=x k}=p k(k=1,2,…)为离散型随机变量X的分布律。分布律也可以用表格的形式来表示,如表2-1所示。

表2-1　离散型随机变量分布律

表2-1直观地表示了随机变量X取各个值的概率的规律,X取各个值的概率值之和为1,可以想象成:概率1以一定规律分布在各个可能值上。

设X是离散型随机变量,它的概率分布是:P{X=x k}=p k,k=1,2,…。如果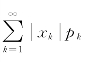有限,定义X的数学期望

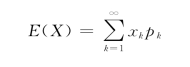
方差

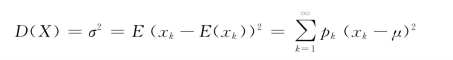
下面介绍两种非常重要的离散型随机变量。