8.7 综合实验
【实验8.1】某品牌饮料30天销量(单位:万瓶)数据如下:
1 023,1 044,1 086,1 099,1 183,1 213,1 239,1 278,1 281,1 326,1 396,1 412,1 436,1 389,1 533,1 566,1 498,1 593,1 620,1 522,1 650,1 699,1 750,1 691,1 796,1 840,1 789,1 847,1 933,1 942
(1)绘制30天饮料销售数据折线图。
(2)在0.05的显著性水平下,利用回归分析预测第31天饮料销量数量,并绘制观测值和预测值的折线图。
(3)分别用k=3和k=5的历史移动平均法预测第31天饮料销售数量,并绘制观测值和预测值的折线图。
(4)设平滑系数α=0.7,试用指数平滑法预测第31天饮料销售数据,并绘制观测值和预测值折线图。
(5)求出最佳阻尼系数,预测第31天饮料销售数据,并绘制观测值和预测值折线图。
【实验步骤】
按列录入数据,如图8-30所示。
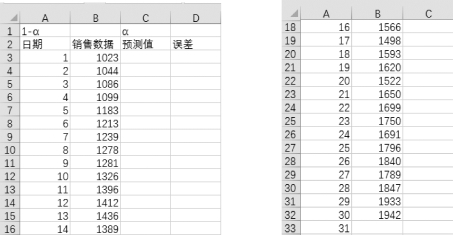
图8-30 录入实验数据
(1)绘制30天饮料销售数据折线图。
选中区域B3:B32,选择“插入”选项卡“图表”组“二维折线图”命令,如图8-31所示。
图8-31 绘制二维折线图
30天饮料销售数据折线图如图8-32所示。
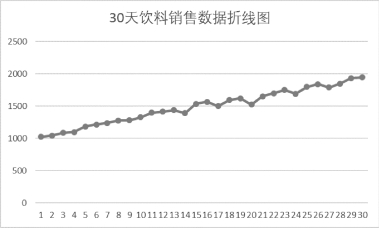
图8-32 30天饮料销售数据折线图
(2)在0.05的显著性水平下,利用回归分析预测第31天饮料销量数量,并绘制观测值和预测值的折线图。选择“数据”选项卡“分析”组“数据分析”命令,在“数据分析”对话框中单击“回归”命令,如图8-33所示。
图8-33 单击回归工具
设置回归参数如图8-34所示。
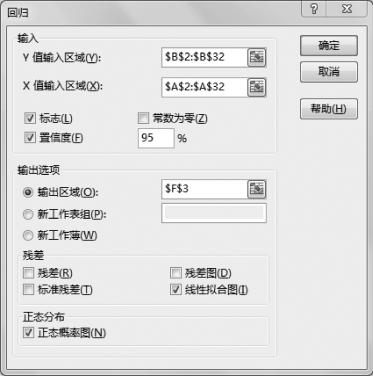
图8-34 设置回归参数
•Y值输入区域:$B$2:$B$32。
•X值输入区域:$A$2:$A$32。
•标志:√。
•置信度:√。
•输出区域:$F$3。
•线性拟合图:√。
•正态分布概率图:√。
回归分析结果如图8-35所示。
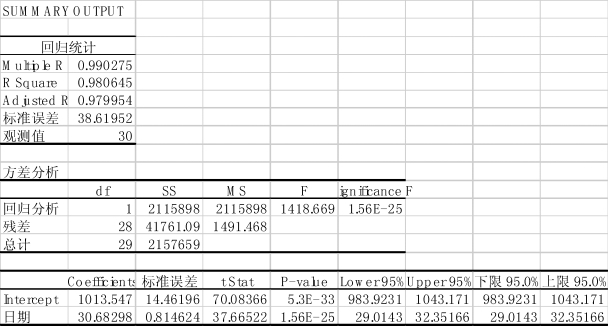
图8-35 回归分析结果
方差分析中的Significance F值为1.56×10-25远远小于0.05,因此自变量对因变量的影响显著。
回归方程为
y=30.683x+1 013.547
常数对应的P-value值为5.3×10-33,变量x对应的P-value值为1.56×10-25,都远小于0.05,因此常数与变量x对因变量y影响显著。
由回归方程,第31天的销量值为
y=30.683×31+1 013.547=1 964.72
线性拟合图如图8-36所示。
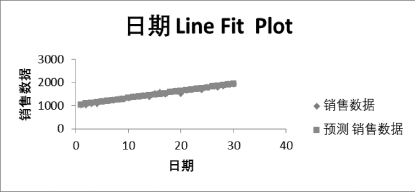
图8-36 线性拟合图
(3)分别用k=3和k=5的历史移动平均法预测第31天饮料销售数量,并绘制观测值和预测值的折线图。选择“数据”选项卡“分析”组“数据分析”中的“移动平均工具”。
①设置k=3时的移动平均工具参数,如图8-37所示。
•输入区域:$B$2:$B$32。
•标志位于第一行:√。
•输出区域:$C$3。
•图表输出:√。
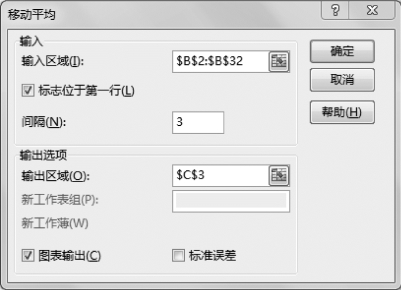
图8-37 设置k=3时移动平均参数
k=3时的移动平均结果如图8-38所示。
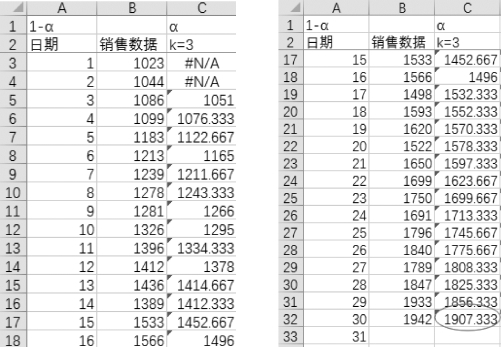
图8-38 k=3时的移动平均结果
k=3时预测值的折线图如图8-39所示。
因此在k=3的条件下,预测第31个月的销售数值为1 907.333。
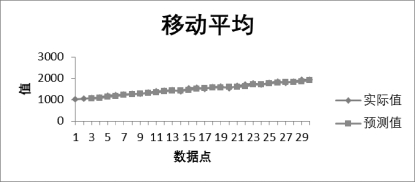
图8-39 k=3时预测值的折线图
②设置k=5时的移动平均工具参数,设置间隔为5,如图8-40所示。(https://www.daowen.com)
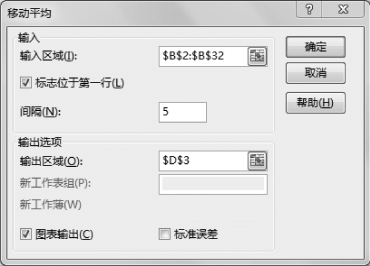
图8-40 设置k=5时移动平均参数
k=5时的移动平均结果如图8-41所示。
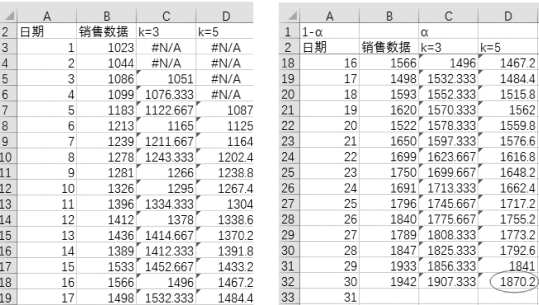
图8-41 k=5时预测值的折线图
k=5时预测值的折线图如图8-42所示。
因此在k=5的条件下,预测第31个月的销售数值为1 870.2。
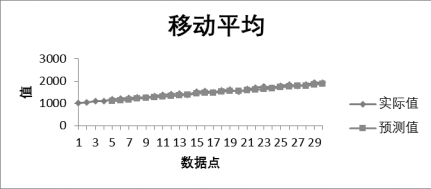
图8-42 k=5时预测值的折线图
(4)设平滑系数α=0.7,试用指数平滑法预测第31天饮料销售数据,并绘制观测值和预测值折线图。
选择“数据”选项卡“分析”组“数据分析”中的“指数平滑”工具,设置“指数平滑”参数,如图8-43所示。
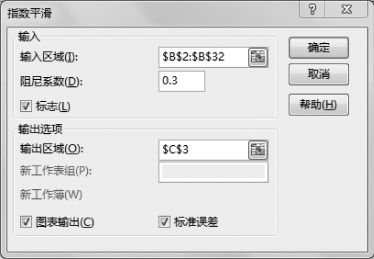
图8-43 设置指数平滑参数
其中输入区域单击原始数据的实际区域,输出区域单击指定的位置,阻尼系数为1-0.7=0.3,指数平滑计算结果如图8-44所示。
指数平滑实际值与预测值折线图如图8-45所示。
第30天的预测值为1 902.772,因此第31天的预测值为
Y 31=0.7×1 942+0.3×1 902.772=1 930.232
也可以利用Excel公式求解“=B32*$B$1+C32*$D$1”进行计算。
(5)求出最佳阻尼系数,预测第31天饮料销售数据,并绘制观测值和预测值折线图。首先设置α的初始值0.7,1-α的值即为“=1-B1”,计算30天销售数据的平均值,对应公式为“=AVERAGE(B3:B32)”,如图8-46所示。
第1天和第2天的预测值均为第1天的实际销量,预测公式为“=B3”。
第3天的预测值的计算公式为
![]()
Excel对应的公式为“=B4*$B$1+C4*$D$1”,向下复制公式至C32。
因为总误差平方和公式为
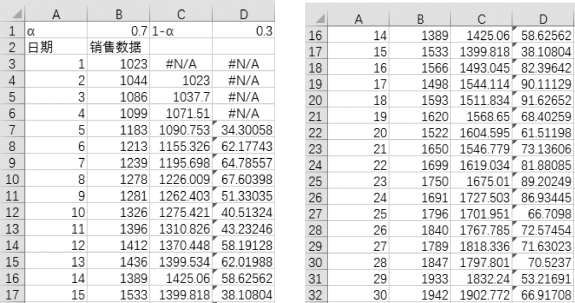
图8-44 指数平滑法结果
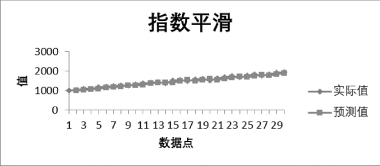
图8-45 指数平滑预测值折线图

图8-46 设置平滑系数初始值并计算对应的阻尼系数与平均值
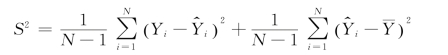
所以第1天的误差公式为“=(B3-C3)2+(C3-$G$2)2”,向下复制公式至单元格D32,计算总误差为30天误差的平方和,即“=SUM(D3:D32)”,如图8-47所示。
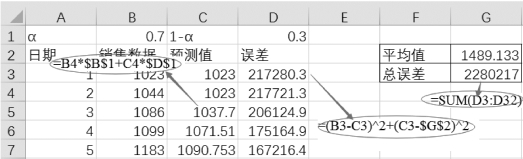
图8-47 计算预测值、误差及总误差的平方和
选择“数据”选项卡“分析”组中的“规划求解”工具,设置规划求解参数,如图8-48所示,设置目标单元格为总误差平方和数值所在单元格,可变单元格为平滑系数所在单元格。
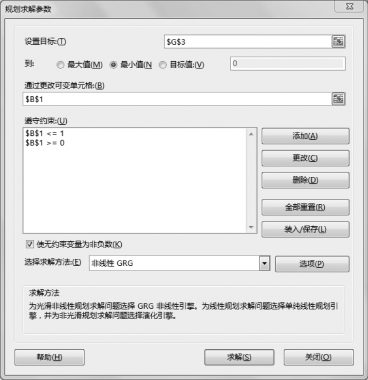
图8-48 设置规划求解参数
添加约束条件,平滑系数0≤α≤1,即对单元格B1进行设置,如图8-49所示。

图8-49 规划求解添加约束条件
规划求解的结果如图8-50所示。
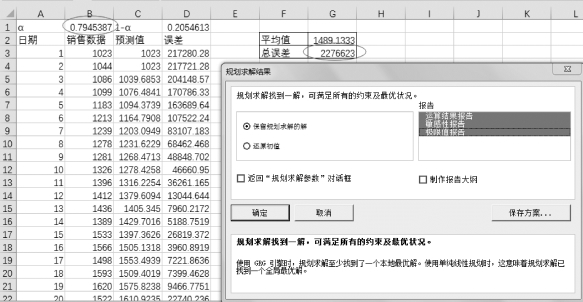
图8-50 规划求解结果
规划求解运算结果报告如图8-51所示。
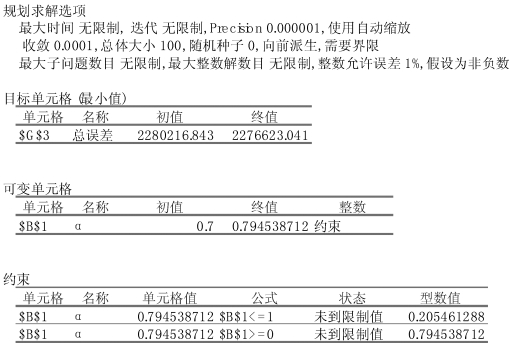
图8-51 规划求解运算结果报告
敏感性报告如图8-52所示。
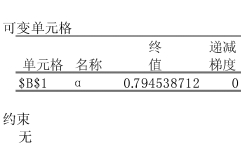
图8-52 规划求解敏感性报告
极限值报告如图8-53所示。
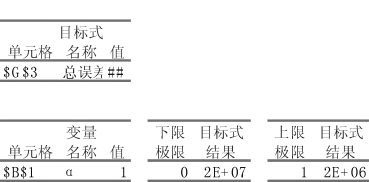
图8-53 规划求解极限值报告
计算第31日的预测销售数量为“=B32*B1+C32*D1”,如图8-54所示。因此可以计算出第31天的预测值为1 936.085。
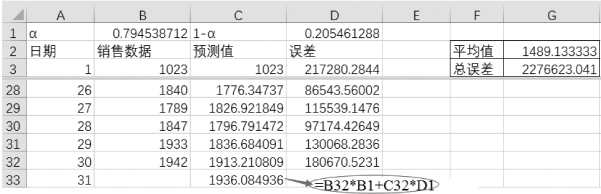
图8-54 预测第31天销量值
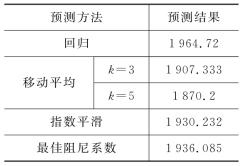
由实验8.1的表8-8可知不同的方法对同样的问题得到不同的预测结果。
表8-8 不同预测方法的结果比较
预测一般是不太准确的。由于预测所研究的是不确定的事物和现象,影响它们的因素多而复杂,很难完全把握,这就决定了预测结果的不准确性。因此预测结果的表达常常是预测区间或预测范围。由于预测对象的不确定性,所以预测结果只能是一个区间,而不需要苛求预测的百分之百正确,只要求将事物的发展规律和趋势基本揭示清楚,为决策提供支持。
