4.4　单侧区间估计

4.4　单侧区间估计

在很多实际问题中,我们并不需要知道区间的上下限,而是只知道上限或者下限中的一种就可以了。例如商品的使用寿命,我们关心的是平均使用寿命的下限,而对于某化学产品的杂质而言,我们更关心的是平均杂质含量的上限,这就是单侧区间估计的问题。

在双侧区间估计中,我们经常用到的是zα/2、tα/2,这是由于在双侧检验中,我们考虑要满足1-α的置信区间,拒绝域分布两侧,一侧各α/2。

而单侧区间估计,对于给定的α(0＜α＜1),μ的置信水平为1-α单侧置信区间为

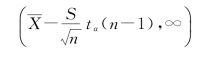
σ2的置信水平为1-α单侧置信区间为

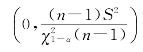
例4.9 从一批灯泡中随机地取5只做寿命实验,测得寿命(单位:h)为

1 050,1 100,1 120,1 250,1 280

设灯泡寿命满足正态分布,在置信区间水平为0.95条件下,求灯泡寿命平均值的单侧置信区间下限。

【实验步骤】

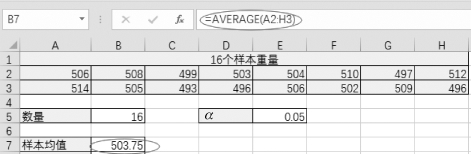
(1)由于总体方差未知,所以首先得通过函数求样本总体均值“=AVERAGE(A2:E2)”(如图4-41所示)与样本标准偏差=STDEV.S(A2:E2)(如图4-42所示)。

图4-41　求样本均值

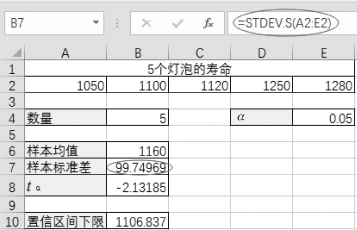
图4-42　求样本标准差

(2)利用T.INV函数求t分布的左尾区间点“=T.INV(E4,B4-1)”(如图4-43所示)。

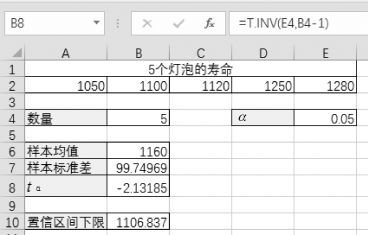
图4-43　返回左尾区间点

注意:T.INV函数返回的是左尾区间点,而T.INV.2T函数返回的是双尾区间点。

(3)根据样本平均值计算置信区间的下限“=B6+B7/4*B8”,如图4-44所示。

注意:置信区间的下限为“=B6+B7/4*B8”,因为T.INV函数返回t分布的左尾区间点已经把“-”号计算进去了。

【结论】灯泡寿命平均值的置信区间水平为0.95的单侧置信区间下限为1 106 h。

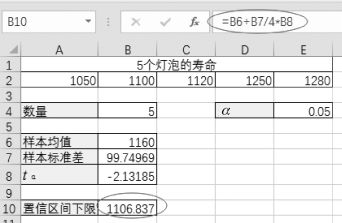
图4-44　求置信区间下限