8.5 最佳阻尼系数
在指数平滑法中,平滑系数越大反应越快,预测不稳定,平滑系数较小将导致预测值的滞后。但是根据给定时间序列的真实值,存在一个最佳的阻尼系数,使得已有数据的真实值和预测值的误差最小,因此在指数平滑时,首先根据时间序列数据,确定最佳阻尼系数,然后进行指数平滑的预测。最佳的阻尼系数使得已有数据的真实值和预测值的误差最小。通常满足预测误差的平方和S 2最小,或满足S最小来计算最佳阻尼系数。
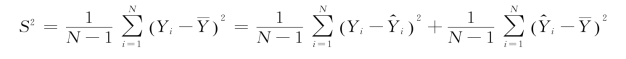
式中:Y i表示第i期的真实值![]() 表示第i期的预测值;Y表示期望,也就是平均值。
表示第i期的预测值;Y表示期望,也就是平均值。
为了快速求出误差平方和的最小值,需要用到Excel提供的规划求解工具。加载宏规划求解工具如图8-17所示。
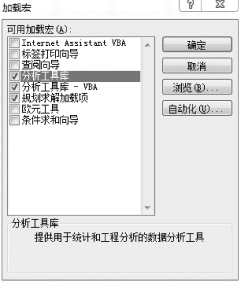
图8-17 加载宏规划求解工具
例8.5 某公司2006—2018年投资总额(单位:万元)数据如表8-7所示。
试确定采用指数平滑法时应选用的最佳阻尼系数,并预测该公司2019年的投资总额。
【实验步骤】
(1)按列录入工作表数据,预设1-α=0.2,那么α的值就是0.8,因此在单元格D1中输入“=1-B1”。计算投资总额的平均值,即在单元格C18中输入“=AVERAGE(C3:C15)”,如图8-18所示。
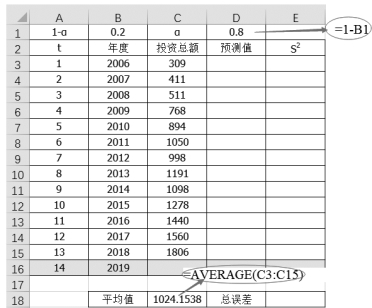
图8-18 预设阻尼系数&计算总体平均值
(2)第1期和第2期的预测值都是第1期的实际投资总额,在单元格D3和D4中都输入“=C3”。
第1期误差S的值按照公式与本期的预测值、投资总额及投资总额的平均值有关,在单元格E3中输入“=SQRT((D3-C3)2+(D3-$C$18)2)”。
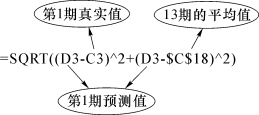
第2期的预测值与第1期的预测值以及第一期的实际值有关,在单元格D4中输入“=C3*$D$1+D3*$B$1”。
分别向下复制公式至单元格D15和E15,如图8-19所示。最后计算总误差平方和,总误差是每期误差平方的和,在单元格E18中输入“=SUM(E3:E15)”。
(3)求误差平方和的最小值。选择“数据”选项卡“分析”组“规划求解”命令,填写规划求解对话框的参数,如图8-20所示。
•设置目标:$E$18,也就是总误差平方和所在单元格。
•单击“最小值”单选按钮。
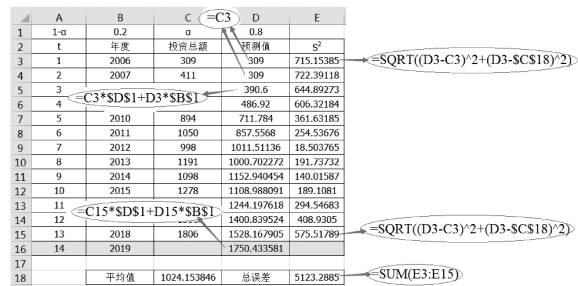
图8-19 计算预测值及误差(https://www.daowen.com)
•添加阻尼系数大于等于0小于等于1的约束条件,在约束条件对话框的右端单击“添加”按钮,在添加约束对话框,添加两个条件,如图8-21所示。
✧$B$1<=1;
✧$B$1>=0。
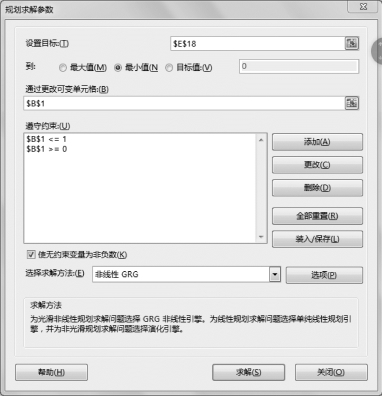
图8-20 规划求解参数设置

图8-21 添加约束条件
•单击“求解”按钮,最优化的结果如图8-22和图8-23所示,最佳阻尼系数为0.017 4。
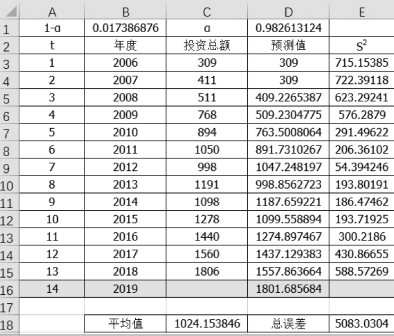
图8-22 规划求解最优解
图8-23 规划求解方案
运算结果报告如图8-24所示。

图8-24 规划求解运算结果报告
敏感性报告如图8-25所示。

图8-25 规划求解敏感性报告
极限值报告如图8-26所示。

图8-26 规划求解极限值报告
【结论】由规划求解我们计算出最佳阻尼系数为0.017 4,那么2019年该公司投资总额的预测值为1 801.69。
