7.2.2 利用回归工具建立一元线性回归方程
Excel 2019提供的回归分析工具通过对一组观察值使用“最小二乘法”直线拟合来执行线性回归分析。该工具可用来分析单个因变量是如何受一个或多个自变量影响的。例如,分析某个运动员的运动成绩与一系列统计因素的关系,如年龄、身高和体重等。首先根据一组成绩数据可确定这三个因素分别在运动成绩测量中所占的比重;然后使用该结果对尚未测量的运动员的成绩作出预测。“回归分析”工具使用工作表函数LINEST。
例7.6 仍然使用例7.5的数据,即为研究某一化学反应过程中温度x(℃)对产品得率Y(%)的影响,测得数据如表7-5所示。试利用回归工具建立温度与得率的线性回归方程。
【回归工具步骤】
(1)选择“数据”选项卡,然后单击“分析”组的“数据分析”工具中的“回归”,如图7-22所示。
图7-22 单击数据分析工具中的回归
(2)设置“回归”参数,如图7-23所示。
•Y值输入区域:$B$1:$B$11,单击实际数据区域。
•X值输入区域:$A$1:$A$11,单击实际数据区域。
•标志:√,根据输入区域是否包含标题行单击。
•置信度:95%,根据实验要求输入。
•输出区域:$D$1。这里可自行单击。
•残差:√。
•残差图:√。
•标准残差:√。
•线性拟合图:√。
•正态概率图:√。
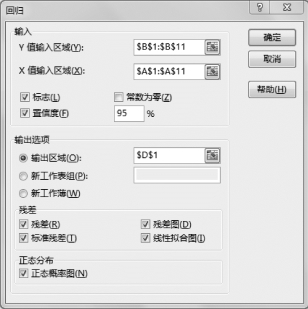
图7-23 回归分析工具参数
(3)回归分析结果如图7-24所示。
①回归汇总输出。
回归汇总输出是回归结果中最重要的部分。包括回归统计信息决定系数、校正决定系数、标准误差、观测值数、方差分析表、回归参数信息。
回归分析结果解析:
•Multiple R:相关系数,分析衡量自变量和因变量的相关程度的大小。
•R Square:决定系数,即R 2。R 2越接近于1,表示自变量对因变量的解释程度越高,表明回归模型与数据吻合得越好。
•Adjusted R Square:校正决定系数。由于用R 2评价拟合模型的好坏具有一定的局限性,即使向模型中增加的变量没有统计学意义,R 2值仍会增大。因此需对其进行校正,从而形成了校正的决定系数(Adjusted R Square)。与R 2不同的是,当模型中增加的变量没有统计学意义时,校正决定系数会减小,因此校正R 2是衡量所建模型好坏的重要指标之一,校正R 2越大,模型拟合得越好,表明回归模型越可靠。
•标准误差:这里的标准误差是估计标准误差,也就是度量各个实际观测点在直线周围的散布状况的一个统计量。
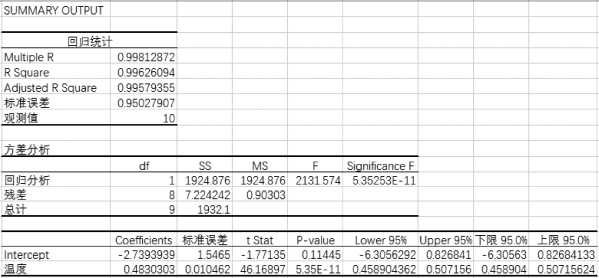
图7-24 回归分析结果
•观测值:实际数据的个数。
•df:自由度。
•SS:样本数据平方和。
•MS:样本数据平均平方和,MS=SS/df。
•F:统计量F的值。
•Significance F:对应的P值。
•Coefficients:对应变量的系数。(https://www.daowen.com)
•标准误差:对应变量的标准误差。
•t Stat:T检验值=回归系数/标准差,用于假设检验,反映两个系数不为零的显著性。
•P-value:T检验值查表对应的P概率,用于假设检验,即真实值为零的可能性。
•Lower 95%:表示根据回归参数计算出的95%置信区间的下限。
•Upper 95%:表示根据回归参数计算出的95%置信区间的上限。
•下限95.0%:表示根据回归参数计算出的95%置信区间的下限。
•上限95.0%:表示根据回归参数计算出的95%置信区间的上限。
【结论】
(1)根据回归统计表可以得到相关系数为0.998 128 72,说明温度与得率显著性相关,呈线性正相关关系。
(2)根据回归统计表可以得到估计的标准误差为0.950 279 07。
(3)根据回归统计表可以得到R 2=0.996 260 94,即1 924.876/1 932.1=0.996 260 94,表明总误差平方和中有99.63%可以由回归方程来解释。
(4)根据回归的汇总输出可以得到线性回归方程为
y=0.483x-2.739 4
(5)Intercept对应的P值为0.114 45>0.05,表明该常数项对回归方程的影响不显著。同样地,Intercept对应的统计量t Start值为-1.771 35∈[-6.305 629 2,0.826 841 33](-6.305 629 2和0.826 841 33分别为Intercept对应的统计量t Start在置信水平为95%的置信区间的上下限),因此可以得到同样的结论,该常数项对回归方程的影响统计上不显著。
(6)“温度”对应的P值为5.35×10-11<0.05,且“温度”对应的统计量t Start值为46.168 97大于置信水平为95%的置信区间的上限0.826 8,落入拒绝域内。以上两项数据均表明该“温度”的系数对回归方程的影响统计上显著。
②残差输出。
残差输出就是每个数据点的预测值与真实值的差值,并计算出正态分布的标准残差数值。残差输出表如图7-25所示。实验点的标准化残差落在(-2,2)区间以外的概率≤0.05。若某一实验点的标准化残差落在(-2,2)区间以外,可在95%置信度将其判为异常实验点,不参与回归直线拟合。
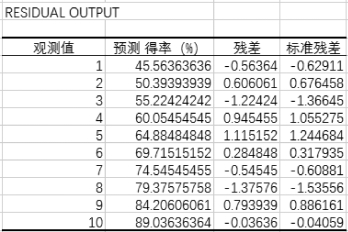
图7-25 残差输出表
③残差图形。
根据前面的步骤计算出来的残差数值对应的残差图形如图7-26所示。

图7-26 温度残差图形
④线性拟合图。
温度线性拟合图如图7-27所示。

图7-27 温度线性拟合图
⑤正态概率图。
正态概率图如图7-28所示。
Excel 2019提供的回归分析工具执行线性回归分析,我们也可以利用数学方法解决非线性回归分析问题。例如,假设自变量x和因变量y满足指数关系,即
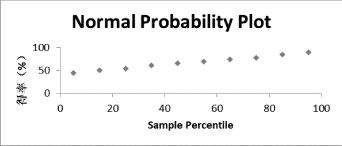
图7-28 正态概率图
y=a e bx
那么可以首先两边同时取对数,
ln y=bx+ln a
将指数关系转换成线性关系之后,再进行回归分析。
