5.4.2 z-检验:双样本均值分析
1.总体方差已知条件下的z-检验
z-检验是一般用于大样本平均值差异性检验的方法。它是用标准正态分布的理论来推断差异发生的概率,从而比较两个平均数的差异是否显著。Excel提供的“z-检验:双样本平均值”分析工具可对具有已知方差的双样本平均值进行z-检验。此工具用于检验两个总体平均值之间不存在差异的零假设,而不是单方或双方的备择假设。如果方差未知,则应该使用工作表函数Z.TEST。
当使用“z-检验:双样本平均值”工具时,应该仔细理解输出。当总体平均值之间没有差别时,“P(Z<=z)单尾”是“P(Z>=ABS(z))”,即与z观察值沿着相同的方向远离0的z值的概率。当总体平均值之间没有差异时,“P(Z<=z)双尾”是“P(Z>=ABS(z)”或“Z<=-ABS(z))”,即沿着任何方向(而非与观察到的z值的方向一致)远离0的z值的概率。双尾结果只是单尾结果乘以2。“z-检验:双样本平均值”工具还可用于当两个总体平均值之间的差异具有特定的非零值的零假设的情况。例如,可以使用此检验来确定两种汽车型号之间的性能差异情况。
下面利用Excel提供的“z-检验:双样本平均值”工具解答例5.7。
【z-检验步骤】
(1)把数据按照“列”的方式排列,如图5-30所示。
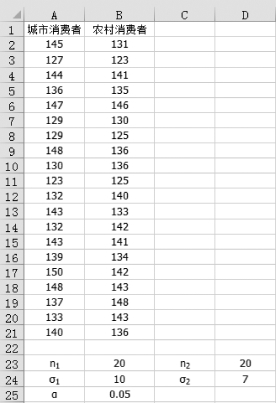
图5-30 按列录入数据
(2)选择“数据”选项卡,然后单击“分析”组的“数据分析”工具中的“z-检验:双样本均值分析”。
(3)设置“z-检验:双样本平均差检验”参数,如图5-31所示。
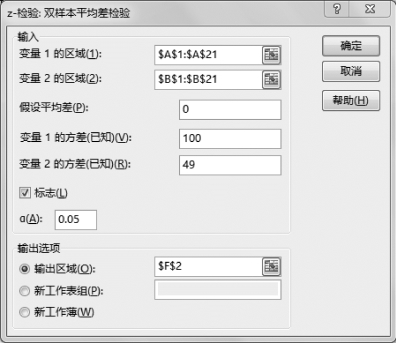
图5-31 “z-检验:双样本平均差检验”参数
•输入变量1的区域:$A$1:$A$21。
•输入变量2的区域:$B$1:$B$21。
•假设平均差:0。
•变量1的方差(已知):100。
•变量2的方差(已知):49。
•标志:√。
•输出区域:$F$2(可自行单击)。
这里需要注意两点:
①输入变量区域中,如果包含标题行,那么需要选中“标志”;如果输入变量区域中不包含标题行,那么不能选中“标志”。
②这里输入的参数是变量的方差而不是标准差,所以输入的是变量1的标准差的平方100和变量2的标准差的平方49。
(4)单击“确定”按钮后,得到“z-检验:双样本均值分析”结果,如图5-32所示。
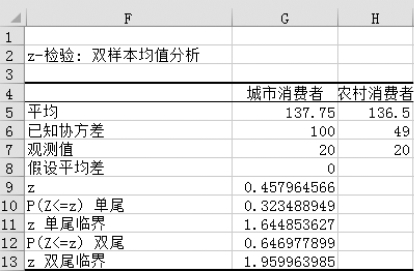
图 “检验:双样本均值分析”结果
(5)可以用两种方法得到结论
方法1 临界值法:单击F16,输入“=IF(G9<G13,"接受H0:μ1=μ2","接受H1:μ1≠μ2")”,得到结论,如图5-33所示。
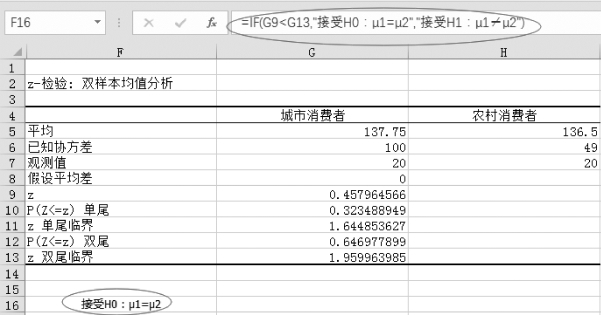
图5-33 临界值法的结论
方法2 P值法:单击F18,输入“=IF(G12<0.05,"接受H1:μ1≠μ2","接受H0:μ1=μ2")”,得到结论,如图5-34所示。
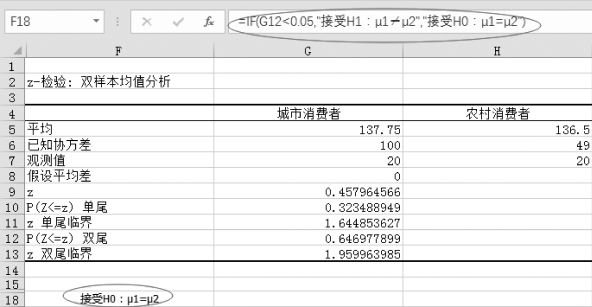
图5-34 P值法的结论
得到结论的方法1明显就是5.3.1节中的临界值法,而方法2是P值法,利用Excel提供的“z-检验:双样本均值分析”使得运算大大简化。
双样本均值分析中,z值0.458 0小于z单尾临界值1.959 96,所以得到结论,城市和农村消费者之间不存在显著性差异。(https://www.daowen.com)
双样本均值分析中,“P(Z<z)双尾值”为0.647 0>0.05,所以得到与上面同样的结论,城市和农村消费者之间不存在显著性差异。
2.总体方差未知条件下的z-检验
如果总体方差均未知,那么和前面的解题思路一样,用样本标准差代替总体标准差。
例5.8 某公司为了分析公司产品的销售情况,调查某两地在消费上是否存在差别。已知两地消费者的消费均服从正态分布,消费标准差均未知,现调查公司从A地客户中抽取50名,从B地客户中随机抽取40名,进行数据统计。统计结果为
A地:99,138,88,127,132,88,115,150,114,126,144,148,150,137,139,125,104,132,87,142,146,111,154,103,110,137,111,119,107,151,155,93,113,123,123,95,99,138,115,135,138,130,93,149,135,109,105,133,149,107
B地:96,132,149,84,114,84,90,97,114,127,128,118,123,127,122,99,113,125,150,94,148,140,96,130,82,100,131,84,80,140,128,127,148,86,122,132,82,91,122,142
试在0.05的显著性水平下判断两地客户之间是否存在差别。
【z-检验步骤】
(1)把数据按照“列”的方式排列,如图5-35所示。
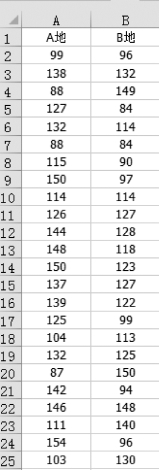
图5-35 按列输入数据
(2)计算A地的基于样本估算标准偏差(忽略样本中的逻辑值和文本),单击单元格E3,输入“=STDEV.S(A2:A41)”。
(3)计算B地的基于样本估算标准偏差,单击单元格G3,输入“=STDEV.S(B2:B36)”,如图5-36所示。
(4)计算A地和B地的样本方差,单击单元格E4,输入“=E3 2”,如图5-37所示。单击单元格G4,输入“=G3 2”,设置单元格为数据,保留3位小数。
(5)选择“数据”选项卡,然后单击“分析”组的“数据分析”工具中的“z-检验:双样本平均差检验”。
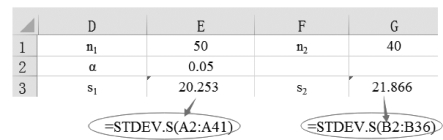
图5-36 计算A地和B地基于样本估算标准偏差
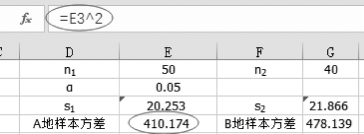
图5-37 计算A地样本方差
(6)设置“z-检验:双样本平均差检验”参数,如图5-38所示。
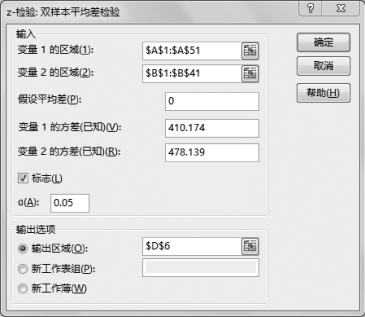
图5-38 “z-检验:双样本平均差检验”参数
•输入变量1的区域:$A$1:$A$51。
•输入变量2的区域:$B$1:$B$41。
•假设平均差:0。
•变量1的方差(已知):410.174。
•变量2的方差(已知):478.139。
•标志:√。
•输出区域:$D$6(可自行单击)。
(7)得到“z-检验:双样本均值分析”结果,如图5-39所示。
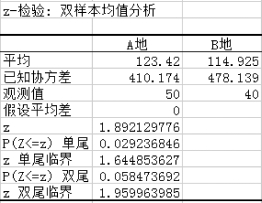
图5-39 “z-检验:双样本均值分析”结果
(8)双样本均值分析中,z值1.892小于z单尾临界值1.959 96,所以得到结论,A地和B地客户不存在显著性差异。
(9)双样本均值分析中,“P(Z<z)双尾值”为0.585>0.05,所以得到与上面同样的结论,A地和B地客户不存在显著性差异。
