4.1.1 总体方差已知情况下均值的置信区间
总体方差已知情况下,若对样本均值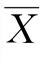
进行标准化,那么标准化后的统计量z满足标准正态分布,即
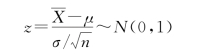
由附录,我们可查知,σ2已知的情况下,均值μ的置信区间为
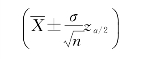
首先介绍Excel中的CONFIDENCE.NORM函数。CONFIDENCE.NORM函数使用正态分布返回总体平均值的置信区间,置信区间为某一范围的值。样本平均值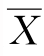
位于此范围的中心,此范围的上下限为
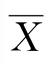±CONFIDENCE.NORM。
CONFIDENCE.NORM函数语法:
CONFIDENCE.NORM(Alpha,Standard_dev,Size)
CONFIDENCE.NORM函数语法具有下列参数:
•Alpha:必需,表示计算置信度的显著性水平参数。
•Standard_dev:必需,表示总体标准差。
•Size:必需,表示样品容量。
下面我们看具体的案例。
例4.1 有一批糖果需要对其平均重量进行估计。已知糖果重量的总体标准差为10 g,在随机抽取60个样本称重后计算出每箱的平均值为500 g,求该仓库中货物平均重量在95%置信水平下的区间估计。
【实验步骤】
(1)通过CONFIDENCE.NORM函数求出区间的半径,双侧置信区间长度为“=CONFIDENCE.NORM(B4,B2,B5)”(如图4-1所示)。
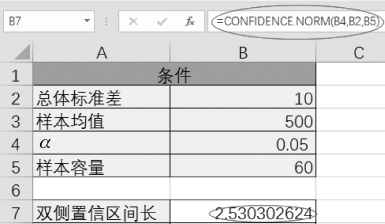
图4-1 利用CONFIDENCE函数求置信区间长度
(2)根据样本平均值计算置信区间的上下限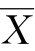
±CONFIDENCE.NORM。其中置信区间上限为“=B3+B7”(如图4-2所示),下限为“=B3-B7”(如图4-3所示)。
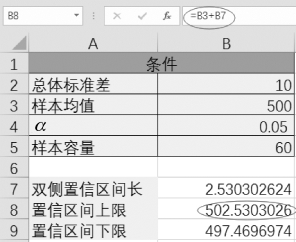
图4-2 置信区间上限
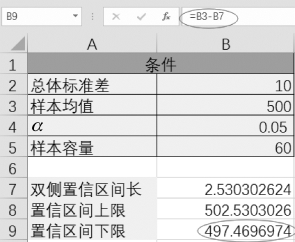
图4-3 置信区间下限
【结论】该仓库中货物平均重量在95%置信水平下的区间估计为(497.47,502.53)。也就是说,以此区间中的任意一个值作为μ的近似值,其误差不大于5.06 g,这个误差估计的可信程度为95%。