7.2.1 利用散点图法建立回归方程
设随机变量Y与x之间存在着某种相关关系。这里,x是可以控制或可以精确观察的变量,如年龄、实验时的温度、施加的压力、电压与时间等。换句话说,我们可以随意指定n个值x 1,x 2,…,x n。因此我们干脆不把x看成是随机变量,而将它当作普通的变量。设Y关于x的回归函数为μ(x)。在实际问题中,回归函数μ(x)一般是未知的,回归分析的任务是根据实验数据去估计回归函数,讨论有关的点估计、区间估计、假设检验等问题。特别重要的是对随机变量y的观察值作出点估计和区间估计。对于x取定一组不完全相同的值x 1,x 2,…,x n,设Y 1,Y 2,…,Y n分别是在x 1,x 2,…,x n处对Y的独立观察结果,记为(x 1,Y 1),(x 2,Y 2),…,(x n,Y n)。
要解决如何利用样本来估计Y关于x的回归函数μ(x)的问题,首先需要推测μ(x)的形式。利用样本来估计μ(x)的问题称为求Y关于x的回归问题。特别地,若μ(x)为线性函数:μ(x)=a+bx,此时估计μ(x)的问题称为求一元线性回归问题。在一些问题中,我们可以由专业知识知道μ(x)的形式。否则,可将每对观察值(x i,y i)在直角坐标系中描出它的相应的点,这种图形称为散点图。散点图可以帮助我们粗略地看出μ(x)的形式。
例7.5 为研究某一化学反应过程中温度x(℃)对产品得率Y(%)的影响,测得数据如表7-5所示。
表7-5 某化学反应过程中温度对产品得率的影响
试利用散点图法建立温度与得率的线性回归方程。
【散点图法步骤】
(1)将数据录入Excel表中,如图7-15所示。
图7-15 按列录入数据
(2)选择“插入”选项卡,然后单击“图表”组的“散点图”选项,如图7-16所示。
(3)选择“图表工具”中的“设计”选项卡,然后单击“数据”组的“单击数据”选项,并单击例7.5中的数据范围:$A$1:$B$11,如图7-17所示。
图7-16 单击插入散点图工具
图7-17 单击图表数据源
(4)出现散点图后,选中散点图的横坐标,单击右键,选择“设置坐标轴格式”,将横坐标最小值设为“90”,最大值设为“200”,如图7-18所示。
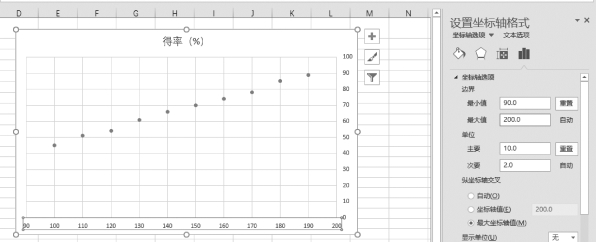
图7-18 设置坐标轴最大值和最小值
注意:第4步主要起到美观的作用,可以跳过。
(5)选择“图表工具”中的“设计”选项卡,然后依次单击“图表布局”组的“添加图表元素”→“趋势线”→“其他趋势线选项”,如图7-19所示。
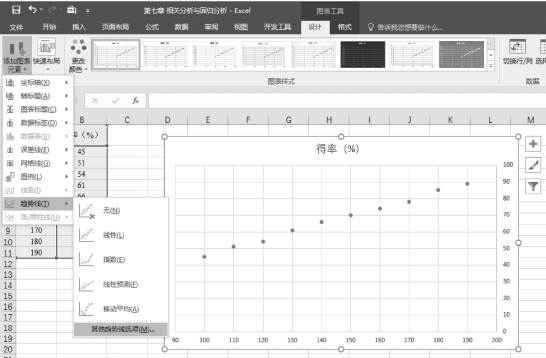
图7-19 插入散点图趋势线
(6)在设置趋势线格式中,选择“线性”;趋势线名称设置为“散点图分析法”;选中“显示公式”和“显示R平方值”复选框,如图7-20所示。
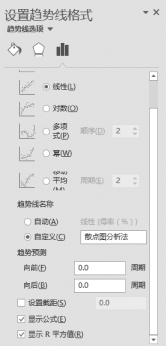
图7-20 显示线性回归方程与拟合度
(7)在散点图中,出现线性趋势线和线性回归方程:y=0.483x-2.739 4,其中R 2=0.996 3,如图7-21所示。
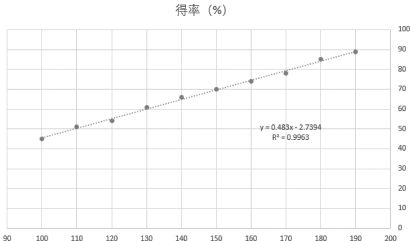
图7-21 利用散点图建立回归方程的结果
【结论】
例7.5中估计μ(x)的问题的一元线性回归方程即为y=0.483x-2.739 4。R 2用来检验回归方程的拟合优度,0≤R 2≤1,其中
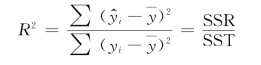
式中:R 2表示判定系数;
表示回归平方和,记为
表示总的离差平方和,记为SST。
拟合度就是说这个模型和你想象的理想情况差多少。如果所有的点都在直线上,一个点也没有离开直线,那么说明拟合度完美,R 2=1。例7.5中的R 2=0.996 3,拟合度相当高,因此接受该回归方程。