2.2.1 一般正态分布
正态分布(Normal Distribution)又称为高斯分布(Gaussian Distribution),是一个在数学、物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力。
连续型随机变量X的密度函数为
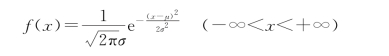
其中,-∞<μ<+∞,σ>0。
正态分布是概率论中最重要的分布,这可以由以下情形加以说明。
(1)正态分布是自然界及工程技术中最常见的分布之一,大量的随机现象都是服从或近似服从正态分布的。可以证明,如果一个随机指标受到诸多因素的影响,但其中任何一个因素都不起决定性作用,则该随机指标一定服从或近似服从正态分布。
(2)正态分布有许多良好的性质,这些性质是其他许多分布所不具备的。
(3)正态分布可以作为许多分布的近似分布。
正态分布能被广泛应用的真正原因是中心极限定理(如图2-2所示)——多个独立统计量的和的平均值符合正态分布。
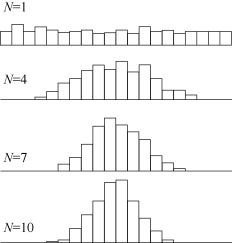
图2-2 中心极限定理
图2-2中,随着统计量个数的增加,它们和的平均值越来越符合正态分布。
根据中心极限定理,如果一个事物受到多种因素的影响,不管每个因素本身是什么分布,它们加总后,结果的平均值就是正态分布。举例来说,人的身高既有先天因素,也有后天因素。男性身高和女性身高都是正态分布,但男女混合人群的身高不是正态分布。每一种因素对男性或者女性身高的影响都是一个统计量,不管这些统计量本身是什么分布,它们和的平均值符合正态分布。
许多事物都受到多种因素的影响,这导致了正态分布的常见。这就会出现一个问题,正态分布是对称的(高个子与矮个子的比例相同),但是很多真实世界的分布是不对称的。比如,财富的分布就是不对称的,在美国财富分布的报告中可以看到,最富有的1%的富人占有财富总量的40%,而底层的70%的人只占有财富总量的7%,即富人的有钱程度远远超出穷人的贫穷程度,即财富分布曲线有右侧的长尾。财富明明也受到多种因素的影响,怎么就不是正态分布呢?原来正态分布只适合各种因素累加的情况,如果这些因素不是彼此独立的,会互相加强影响,那么就不是正态分布了。统计学家发现,如果各种因素对结果的影响不是相加,而是相乘,那么最终结果不是正态分布,而是对数正态分布,即x的对数值log(x)满足正态分布。
尽管正态变量的取值范围是(-∞,+∞),但它的值落在(μ-3σ,μ+3σ)内几乎是肯定的事,这就是“3σ”法则。
•函数曲线下68.268 949%的面积在(μ-σ,μ+σ)范围内。
•函数曲线下95.449 974%的面积在(μ-2σ,μ+2σ)范围内。
•函数曲线下99.730 020%的面积在(μ-3σ,μ+3σ)范围内。
•函数曲线下99.993 666%的面积在(μ-4σ,μ+4σ)范围内。
Excel 2019提供两个正态分布函数。
1.NORM.DIST函数
NORM.DIST函数返回指定平均值和标准偏差的正态分布函数。
NORM.DIST函数语法:
NORM.DIST(x,mean,standard_dev,cumulat ive)
NORM.DIST函数语法具有下列参数:
•x:必需,需要计算其分布的数值。(https://www.daowen.com)
•mean:必需,分布的算术平均值。
•standard_dev:必需,分布的标准偏差。
•cumulative:必需,决定函数形式的逻辑值。
✧如果cumulative为TRUE(1),则NORM.DIST返回累积分布函数;
✧如果cumulative为FALSE(0),则返回概率密度函数。
注意:Excel早期的正态分布函数是NORMDIST(x,mean,standard_dev,cumulative)。
2.NORM.INV函数
NORM.INV函数返回指定平均值和标准偏差的正态累积分布函数的反函数值。
NORM.INV函数语法:
NORM.INV(probability,mean,standard_dev)
NORM.INV函数语法具有下列参数:
•probability:必需,对应于正态分布的概率。
•mean:必需:分布的算术平均值。
•standard_dev:必需,分布的标准偏差。
备注:
①如果mean=0且standard_dev=1,则NORM.INV使用标准正态分布(请参阅函数NORM.S.INV)。
②如果已给定概率值,则NORM.INV使用NORM.DIST(x,mean,standard_dev,TRUE)=probability求解数值x。因此,NORM.INV的精度取决于NORM.DIST的精度。
③Excel早期的正态分布函数是NORMINV(probability,mean,standard_dev)。
例2.4 将一个温度调节器放置在贮存着某种液体的容器内,调节器整定在90℃,液体的温度X是一个随机变量,且X~N(90,0.52)。求X小于89℃的概率,以及99%的概率下温度不会超过多少?
【解答】
(1)在选中单元格中输入“=NORM.DIST(89,90,0.5,1)”,显示结果为0.022 75。即若d=90℃,X小于89℃的概率是0.022 75。
NORM.DIST函数解析:
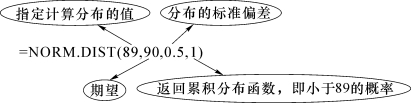
(2)在选中单元格中输入“=NORM.INV(0.99,90,0.5)”,显示结果为91.16。即在99%的概率下该温度调节器的温度不会超过91.16℃。
NORM.INV函数解析:

