7.1.2 相关系数的检验
相关系数的检验目的是检验总体两变量间的线性相关性是否显著,对于一个二元总体,提出假设
H 0:两变量无关(ρ=0);H 1:两变量相关(ρ≠0)
如果样本容量n≤30,那么该检验属于小样本相关系数为0的检验,即统计量为自由度为n-2的t分布,对应的t统计量为
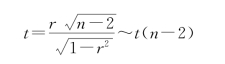
例7.3 小样本相关系数为0的检验
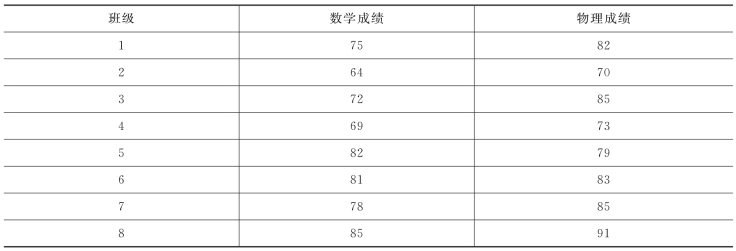
某学校希望知道物理成绩与数学成绩是否存在相关性,因此从全校学生中随机抽取8个班级,统计后的数学与物理平均成绩如表7-4所示,试在0.05的显著性水平下判断数学成绩与物理成绩间是否存在相关性。
表7-4 各班数学与物理平均成绩(单位:分)
【相关系数为0的小样本检验步骤】
首先提出假设
H 0:两变量无关(ρ=0);H 1:两变量相关(ρ≠0)
因为各有8个数据,所以例7.3属于小样本相关系数为0的检验,统计量为自由度为n-2的t分布,对应的t统计量为
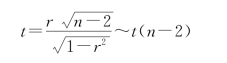
(1)首先录入数据,并录入n=8,α=0.05,如图7-7所示。
(2)计算样本相关系数,在单元格B14中输入“=CORREL(B2:B9,C2:C9)”,如图7-8所示。
(3)计算统计量t,在单元格B15中输入“=B14*SQRT(B11-2)/(1-B14 2)”,如图7-9所示。
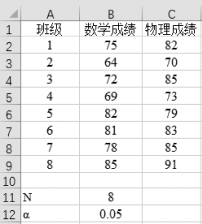
图7-7 录入数据
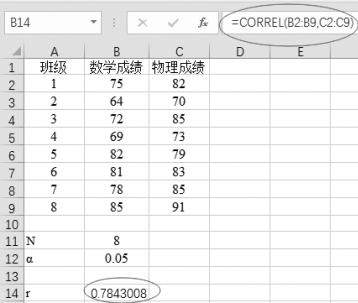
图7-8 计算样本相关系数
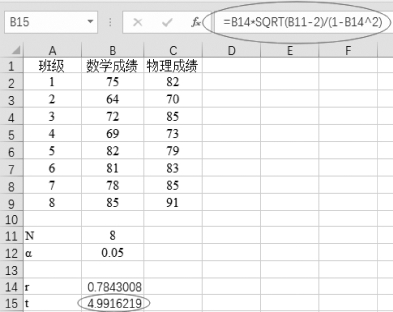
图7-9 计算统计量的值
(4)计算临界值tα/2,在单元格B16中输入“=T.INV.2T(B12,B11-2)”,如图7-10所示。
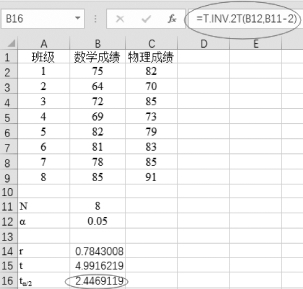
图7-10 计算临界值
【结论】
因为统计量t的值4.992大于t的临界值2.447,所以t值落在了拒绝域,因此接受备择假设,数学成绩与物理成绩相关。
在结论单元格中输入“=IF(ABS(B15)＜B16,"数学成绩与物理成绩无关","数学成绩与物理成绩相关")”。
上面讨论的是小样本的情况,如果样本容量n＞30,那么该检验属于大样本相关系数为0的检验,应采用标准正态分布进行检验,对应的z统计量为
例7.4 大样本相关系数为0的检验
某公司跟踪其商品在城市和农村的销售情况,统计的数据如下。
城市:114,116,104,100,97,118,83,115,94,108,128,93,97,107,108,107,98,83,105,93,111,107,88,98,76,115,118,112,116,121,97,126,98,122,97,120
农村:131,102,87,129,143,117,107,96,116,140,120,122,113,117,137,123,131,119,113,132,128,117,110,110,129,125,96,95,126,123,102,110,117,135,89,99
试在0.05的显著性水平下判断两地区的销量是否显著相关。
【相关系数为0的大样本检验步骤】
首先提出假设
H 0:两变量无关(ρ=0);H 1:两变量相关(ρ≠0)
因为各有36个数据,所以例7.4属于大样本相关系数为0的检验,统计量为
(1)首先录入例7.4数据,并录入n=36,α=0.05,如图7-11所示。
(2)计算样本相关系数,在单元格B42中输入“=CORREL(A2:A37,B2:B37)”,如图7-12所示。
(3)计算统计量z,在单元格B43中输入“=B42*SQRT(B39-1)”,如图7-13所示。
(4)计算临界值zα/2,在单元格B44中输入=NORM.S.INV(B40/2),如图7-14所示。
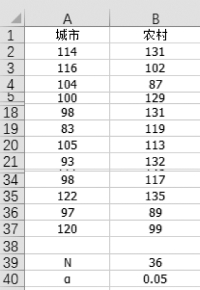
图7-11 按列录入数据
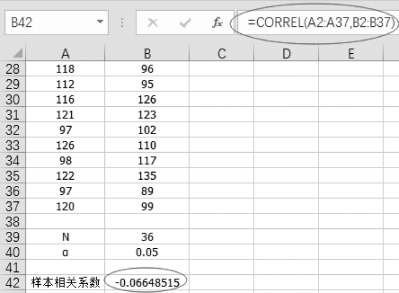
图7-12 计算样本相关系数
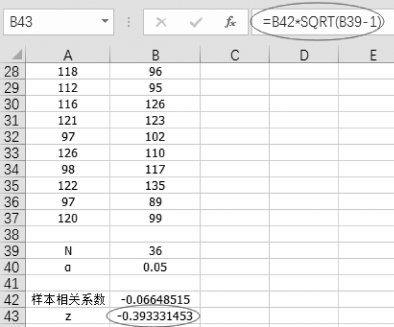
图7-13 计算统计量z的值
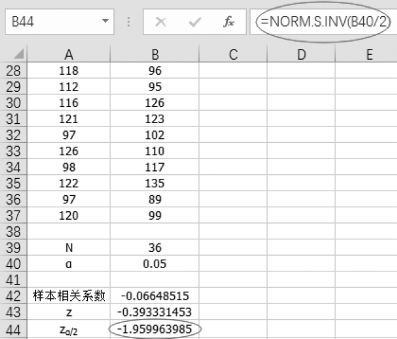
图7-14 计算z的临界值
【结论】
在结论单元格中输入“=IF(ABS(B43)＜ABS(B46),"城市与农村的销售量无关","城市与农村的销售量相关")”。因为统计量z的绝对值0.393 3小于z的临界值的绝对值1.960,所以z值没有落在拒绝域,即无法拒绝原假设,因此城市与农村的销售量无关。