6.2.1 无重复双因素方差分析
无重复双因素方差分析假定因素A和因素B的效应之间是相互独立的,不存在相互关系。无重复实验只需要检验两个因素对实验结果有无显著影响。
如果在处理实际问题时,我们已经知道不存在交互作用,或已知交互作用对实验的指标影响很小,则可以不考虑交互作用。此时,即使k=1,也能对因素A、因素B的效应进行分析,现设对于两个因素的每一组合(A i,B j)只做一次实验,所得结果如表6-4所示。
表6-4 双因素无重复随机实验
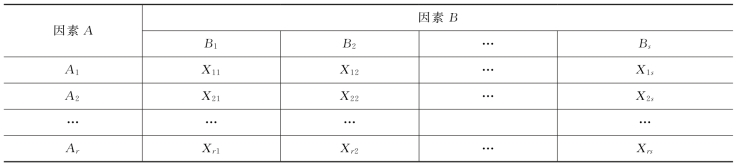
对应的无重复双因素实验的方差分析如表6-5所示。
表6-5 双因素无重复实验方差分析表
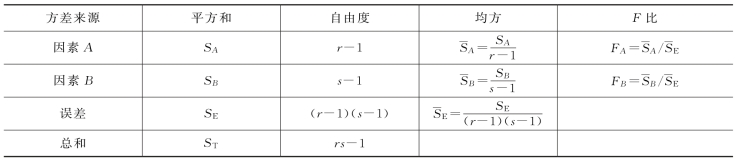
Excel在数据分析中提供了“方差分析:无重复的双因素”工具。此分析工具可用于分析按两个不同的维度归类的数据。但是,对于此工具,假设每个配对只有一个观测值(每个{因素A,因素B}配对)。
例6.2 表6-6给出了在某5个不同地点、不同时间空气中颗粒状物(以mg/m3计)的含量数据。
表6-6 不同地点、不同时间空气中颗粒状物的含量
试在显著性水平α=0.05下检验:
(1)在不同时间下颗粒状物含量的均值有无显著差异;
(2)在不同地点下颗粒状物含量的均值有无显著差异。
【无重复双因素方差分析步骤】
(1)将实验数据录入Excel表中,注意按照时间和地点按列(或行)录入,如图6-4所示。
图6-4 实验数据录入
(2)选择“数据”选项卡,然后单击“分析”组的“数据分析”工具中的“方差分析:无重复双因素分析”,如图6-5所示。
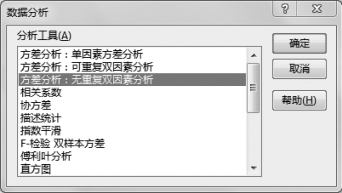
图6-5 单击“方差分析:无重复双因素分析”
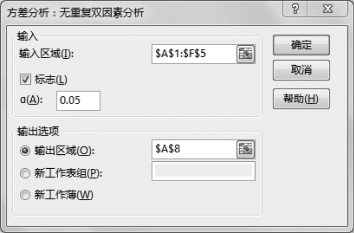
(3)设置“方差分析:无重复双因素分析”参数,如图6-6所示。
图6-6 “方差分析:无重复双因素分析”参数设置
•输入区域:$A$1:$F$5,这里单击实际数据区域。
•标志:√。
•α:0.05。根据实验要求的显著性水平填写。
•输出区域:$A$8。这里可自行单击。
(4)无重复双因素方差分析结果如图6-7和图6-8所示。
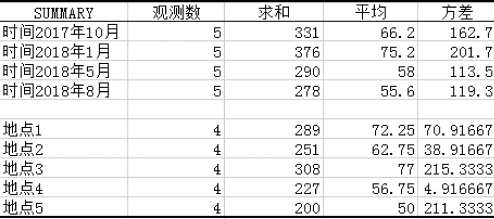
图6-7 无重复双因素均值与方差
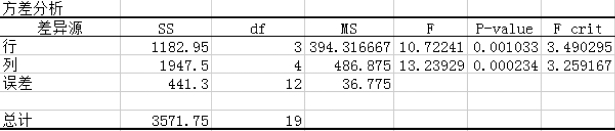
图6-8 无重复双因素方差分析
无重复双因素方差分析结果解释:
•在SUMMARY(摘要)中,分别计算出4个时间和5个地点对应的观测数、和、平均值与方差。
•方差分析:
✧SS表示离均差平方和,也就是变量中每个数据点与变量均值差的平方和;
✧df表示自由度;
✧MS表示均方,MS的值等于对应的SS除以df;
✧F表示F统计量,是方差分析中用于假设检验的统计量,其值等于处理的MS除以误差的MS;
✧P-value表示概率值;
✧F crit表示在0.05的显著性水平下F的临界值。
【结论】
(1)观察行P-value的值,样本P-value=0.001 03＜0.05,落入拒绝域,因此可以得到结论,在不同时间下颗粒状物含量的均值有显著差异。
(2)观察列P-value的值,样本P-value=0.000 234＜0.05,落入拒绝域,因此可以得到结论,在不同地点下颗粒状物含量的均值有显著差异。