4.1　单个正态总体的区间估计

对于一个未知参数,很多情况下我们并不需要知道它具体的估值,显而易见,通过样本估计出来的具体值,一定不那么“准确”。所以在实际应用中,我们更希望估计出这个未知参数的一个范围,并知道这个范围包含该参数真值的可信程度。这个范围区间的估计在统计学中被称为区间估计,这个区间即为置信区间。

置信区间的定义:设总体X的分布函数中含有一个未知参数θ,θ∈D(其中D是θ可能取值的范围),对于给定的值α(0＜α＜1),若由来自X的样本X 1,X 2,…,X n确定的两个统计量和,对于任意θ∈D满足

则称随机区间是θ的置信水平为1-α的置信区间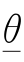和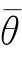分别称为置信水平为1-α的双侧置信区间的置信上限和置信下限,1-α称为置信水平。

换一个通俗的解释,如果我们假定的α=5%,那么所估计的这个参数的真值有95%的概率落在置信区间内。一般地,我们取α为5%或者1%。

对于正态分布,正态总体均值、方差的置信区间与单侧置信限(0＜α＜1)满足附录的关系。

假设已经给定的置信水平为1-α,X 1,X 2,…,X n为总体N(μ,σ2)的样本。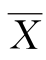和S 2分别为样本均值和样本方差。