9.1.1 距离分析法
聚类分析常常采用描述个体对之间的接近程度的指标来进行分类。例如,选择个体之间的“距离”来进行分类,设定“距离”越短的两个个体越具有相似性,把距离接近的个体归于一类。这里的距离也是一个广泛的定义,常用的距离方法有以下5种。
(1)绝对距离
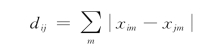
(2)欧氏距离
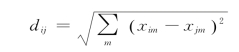
欧氏距离即大家最常用的两点之间直线最短的概念。
(3)马哈拉诺比斯距离
![]()
马氏距离中引入协方差参数(表征的是点的稀密程度)来平衡两个类别的概率。马氏距离的特点是结果与量纲无关,排除变量之间相关性的干扰。若协方差矩阵是对角矩阵,公式变成了标准化欧氏距离。
(4)切比雪夫距离
切比雪夫距离定义为两个点之间各坐标数值差的最大值。以点(x1,y 1)和(x2,y 2)为例,它们的切比雪夫距离为
![]()
(5)海明距离
两个码字的对应比特取值不同的比特数称为这两个码字的海明距离。例如10101和00110从第一位开始依次有第一位、第四位、第五位不同,则海明距离为3。
对一个实际分类问题选定一种最能刻画样本间相似、相近程度的距离的过程,也被称为分类统计量。将统计量进行分类以后,接下来就是制定分类规则。当然将全部样品合并成一类并不是我们的目的,我们的目的在于,通过上述逐渐并类的过程,有可能找到最佳的分类方案。具体地讲,通过上述并类过程,我们可以根据聚类的先后以及并类时两类间的距离,画出能直观反映各样品之间相近和疏远程度的聚类图。根据这张聚类图有可能找到最合适的分类方案。为了实现上述思想,必须考虑类与类之间的距离如何定义。在上述聚类过程的第一步,由于每一类中的样品都只有一个,因此可以用样品间的距离来定义类间的距离。可是第一次并类以后,某些类中所包含的样品数将多于一个,在这种情况下,如何合理地定义类间的距离非常重要。实际上,用不同的方法定义类间距离就产生了不同的系统聚类的方法。
下面介绍距离法聚类的具体步骤。
假设样本i到样本j的距离d ij与样本j到样本i的距离相等。
(1)计算样本两两距离,由于初始状态每个样本自成一类,此时Dij=d ij,得到初始距离阵D(0),第i行和第j列一样,都称为一个类Gi。
(2)找出D(0)的非对角线最小元素,假设为D pq,则将Gp与Gq合并成一个新类,记为Gr,即Gr={Gp,Gq} 。
(3)给出计算新类与其他类的距离公式:D kr=min{ Dkp,D kq} ,D(0)中第p、q行及p、q列均利用上面的方法并成一个新行及新列,新行及新列对应Gr,所得到的矩阵记为D(1)。
(4)对D(1)重复上述对D(0)的(2)、(3)步骤得D(2),如此下去,直到所有的元素并成一类为止。如果某一步D(k)中非对角线最小的元素不止1个,则对应这些最小元素的类可以同时合并。
1.最短距离法
最短距离法就是对于距离法中的类的距离定义为两类最近样本的距离。最短距离法聚类的基本思想是:首先是n个样本各自成一类,然后规定类与类之间的距离,单击距离最小的2类合并成1个新类,计算新类与其他类的距离,再将距离最小的2类进行合并,这样每次减少1类,直到达到所需的分类数或所有的样本都归为1类为止,其中距离系数都是正数,而且2类之间的距离系数越小则认为两类间的关系越密切。
定义类i与j之间的距离为两类最近样品的距离:
![]()
若类p与q合并成一个新类记作r,则k与r的距离为
![]()
例9.1 我国油茶主产区集中分布在湖南、江西、广西、浙江、福建、广东、湖北、贵州、安徽、云南、重庆、河南、四川和陕西14个省(区、市)的642个县(市、区),表9-1为2017年全国油茶主产区分布范围统计表(单位:万亩),要求使用最短距离法对样本进行聚类分析,并将油茶产地分布范围分为“很集中”、“集中”、“较集中”与“一般”4个类别。
表9-1 2017年全国油茶主要产区分布范围统计

【实验步骤】
(1)将表9-1的数据录入Excel中,并利用标准差规格化法,将原始数据标准化。
①计算原始数据的平均值,选中单元格E2,输入“=AVERAGE(B2:B15)”。
②计算原始数据的标准差,选中单元格F2,输入“=STDEV.S(B2:B15)”。
③标准化过程,选中单元格C2,输入“=(B2-$E$2)/$F$2”,复制单元格C3至C15,如图9-1所示。
(2)利用“选择性粘贴中”的“数值”功能,将省份和标准化后的数据复制到“最小距离法” 的表中,如图9-2所示。
在表“最小距离法”中,将标准化后的数据,利用“选择性粘贴”中的“转置”,将A、B列的数据复制到2、3行,并将其美化,如图9-3所示。
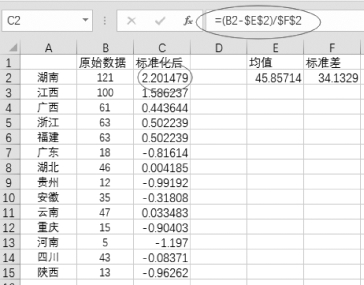
图9-1 原始数据标准化
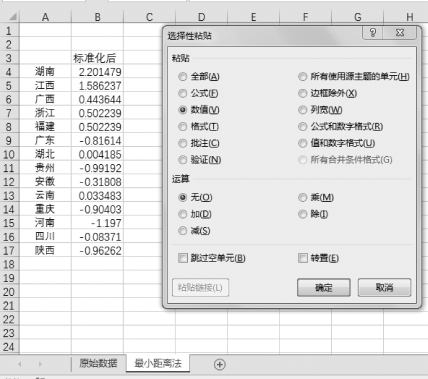
图9-2 选择性粘贴只粘贴数值
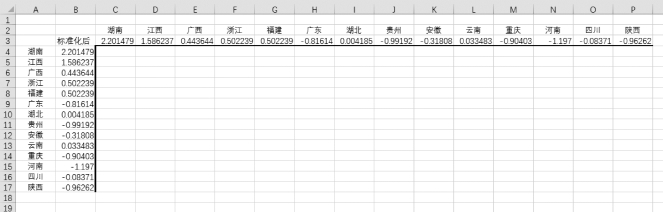
图9-3 原始数据标准化
(3)本例中利用欧氏距离计算标准化数据之间的距离,选中单元格C4,输入“=ABS($B4-C$3)”(如图9-4所示),注意相对引用中$符号的位置,复制公式覆盖整张表(如图9-5所示)。
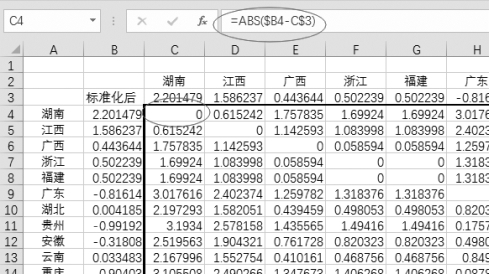
图9-4 欧氏距离计算公式
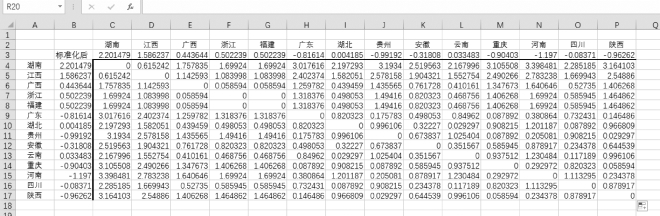
图9-5 欧氏距离计算结果
(4)选中区域C4:P17,依次选择“开始”选项卡→“样式”组→“条件格式”→“项目选取规则”→“其他规则”命令,如图9-6所示。
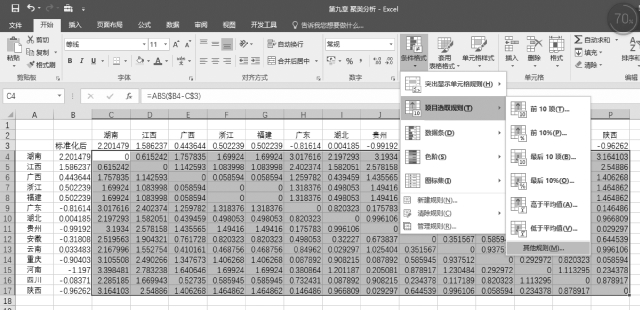
图9-6 条件格式设置
如图9-7所示,在“新建格式规则”对话框中的编辑规则说明中,单击“后”“15”,格式中单击填充为“黄色”,也就是让后15个距离最小的值突出显示,如图9-8所示。
图9-7 新建格式规则
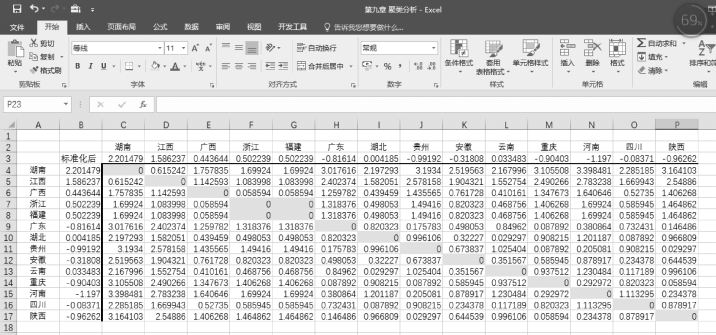
图9-8 条件格式显示结果
结果显示除了对角线上的14个0以外,浙江与福建的距离最小。
(5)在单元格Q2和单元格A18中均输入“浙江福建”,注意“浙江”与“福建”中间可用Alt键+Enter键进行强制分行,如图9-9所示。
单击单元格C18,输入“=MIN(C7,C8)”,在区域D18:P18中复制公式;单击单元格Q4,输入“=MIN(F4,G4)”,在区域Q4:Q18中复制公式,结果如图9-10所示。
(6)为了方便读者阅读和查看实验数据,我们将区域A2:Q18中的所有数据利用“选择性粘贴”中的“数值”,将其复制到区域A21:Q37中,如图9-11所示。注意这里的公式已经转换为数值了。
注意:此步骤仅为了方便读者查看电子数据,读者自行实验时可省略。
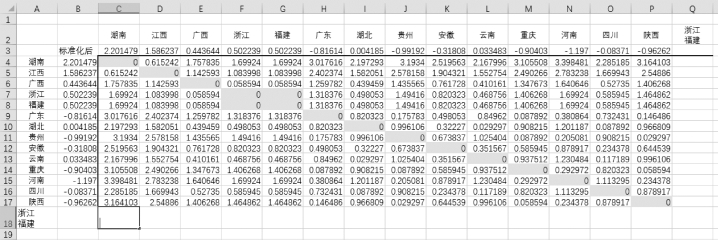
图9-9 生成“浙江、福建”新类
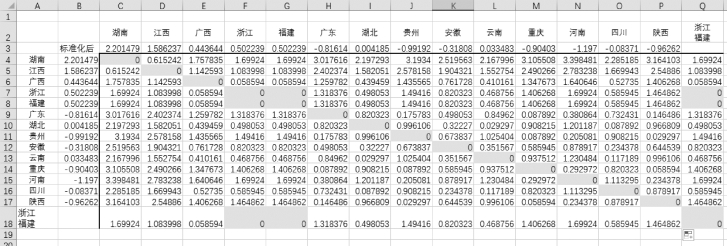
图9-10 用最短距离法计算新类与其他类之间的距离
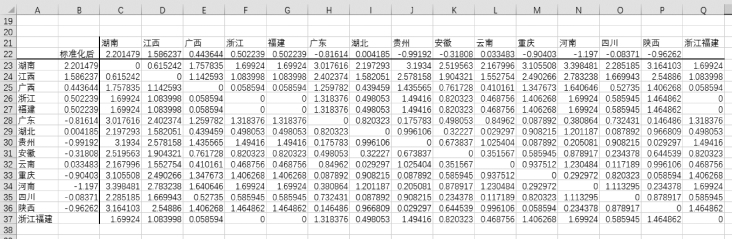
图9-11 移动数据
删除“浙江”和“福建”所在的行与列,此时浙江与福建就合并为一个新类,如图9-12所示。
(7)重复步骤(4),注意每一次在条件格式中单击后N项,N=实际类数+1,例如在图9-13中有13类,那么N=14。
根据图将“陕西”与“贵州”合并为一个新类,并重复步骤(5),形成新的表,如图9-14所示。
将所有数值复制、单击性粘贴为“数值”后,删除“陕西”与“贵州”的行与列,得到“陕西、贵州”的新类,如图9-15所示。
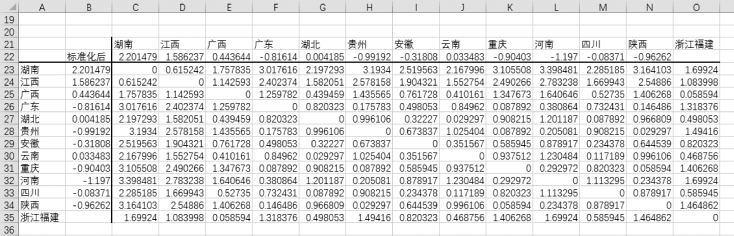
图9-12 删除“浙江”和“福建”列形成新表
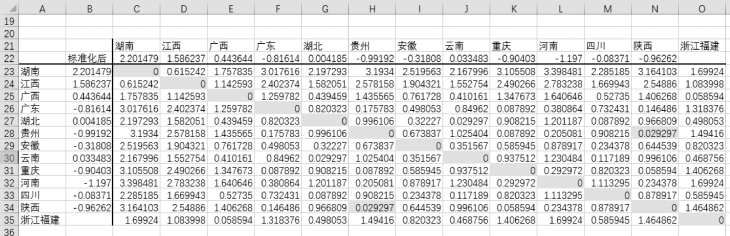
图9-13 条件格式设置找出最小距离的两类
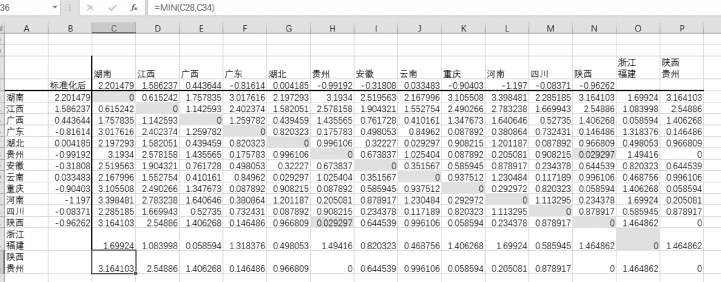
图9-14 将“陕西”与“贵州”合并为一个新类(https://www.daowen.com)
(8)重复步骤(4)和(5),最后得到4类时停止(如图9-16~图9-22所示)。注意,由于需要删除数据,因此在每次计算新类与其他类之间的距离后,需要将新类距离中的公式复制粘贴为数值形式。
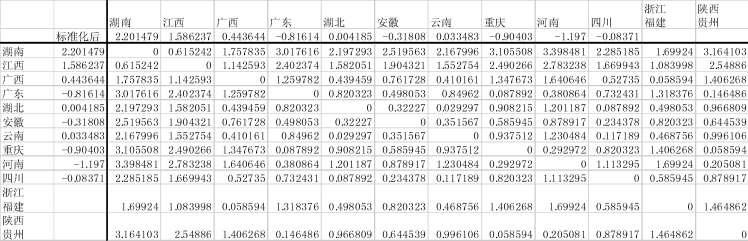
图9-15 将“陕西”与“贵州”原类删除
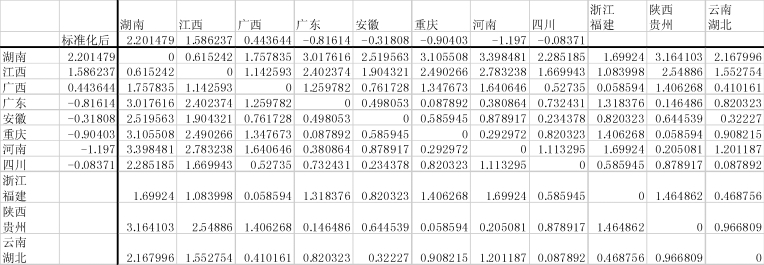
图9-16 将“云南”与“湖北”合并为一个新类
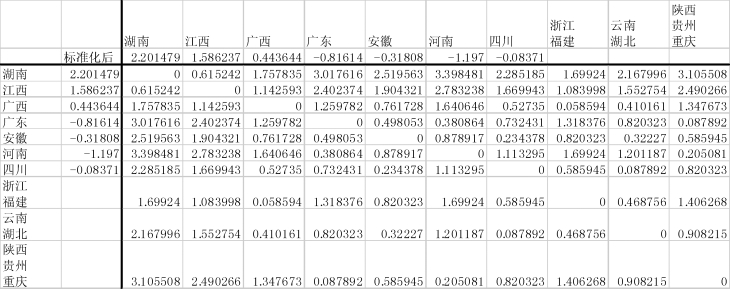
图9-17 将“陕西、贵州”与“重庆”合并为一个新类
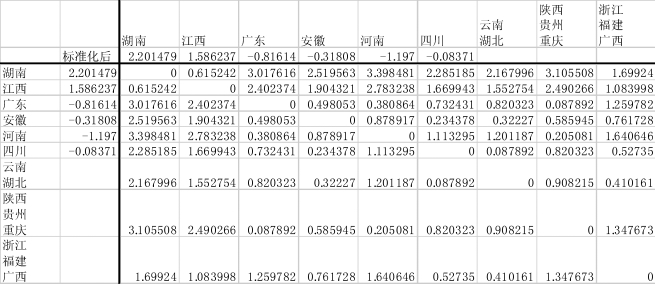
图9-18 将“浙江、福建”与“广西”合并为一个新类
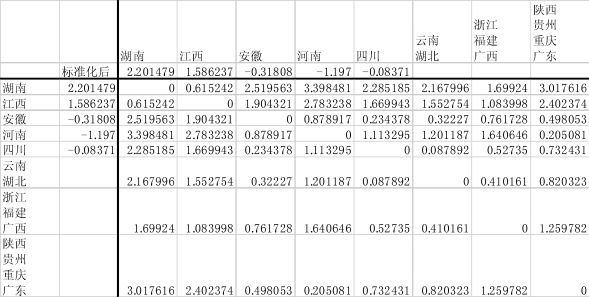
图9-19 将“陕西、贵州”与“重庆、广东”合并为一个新类
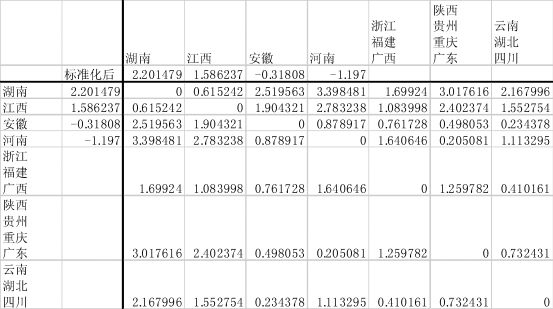
图9-20 将“云南、湖北”与“四川”合并为一个新类
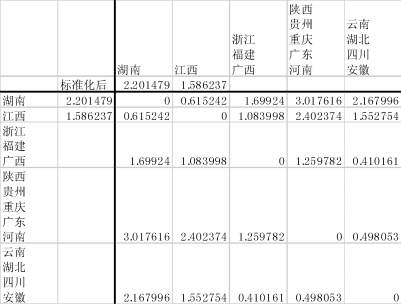
图9-21 将“陕西、贵州、重庆、广东”与“河南”合并为一个新类,将“云南、湖北、四川”与“安徽”合并为一个新类
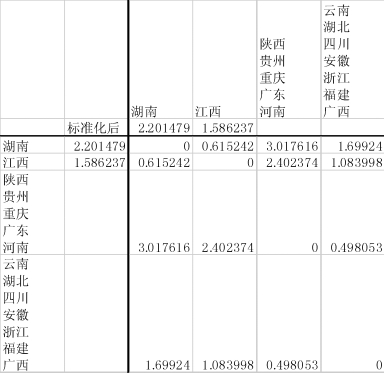
图9-22 将“云南、湖北、四川、安徽”与“浙江、福建、广西”合并为一个新类
【结论】油茶产地分布范围最终分为4类,再根据原始数值很容易推断出油茶产地分布的分类,如表9-2所示。
表9-2 油茶产地分布分类

图谱分析如图9-23所示。
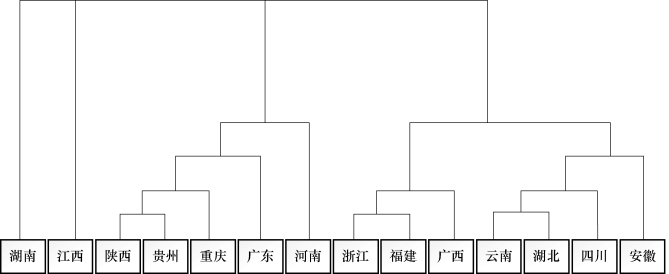
图9-23 最小距离法油茶产地分布图谱分析
在实验过程中,我们可以看到,最小距离法分类在计算前并不能判断能将样本分为几类,也无法判断每类会有多少个样本。按照最小距离法的步骤依次循环,直到最后分为需要的4类,再主动停止操作。
2.最长距离法
最长距离法和最短距离法的差别就在于类的距离的定义。最短距离法定义类i与j之间的距离为两类样本的最短距离,而最长距离法则定义类i与类j之间的距离为两类样本的最长距离。
最长距离法聚类的基本思想是:首先是n个样本各自成一类,然后规定类与类之间的距离,单击距离最小的2类合并成1个新类,计算新类与其他类的距离,再将距离最小的2类进行合并,这样每次减少1类,直到达到所需的分类数或所有的样本都归为1类为止,其中距离系数都是正数,而且2类之间的距离系数越小则认为两类间的关系越密切。
定义类i与j之间的距离为两类最近样品的距离:
![]()
若类p与q合并成一个新类记作r,则k与r的距离为
![]()
例9.2 最长距离法的应用
例9.2仍以表9-1的数据来进行实验,要求使用最长距离法对样本进行聚类分析,将油茶产地分布范围分为“很集中”、“集中”、“较集中”与“一般”4个类别。最长距离法的差别在于合并新类时,计算两类之间的距离由计算最小值变为计算最大值。
【实验步骤】
步骤(1)~(4)与例9.1完全一致,我们从第(5)步开始。
(5)在单元格Q2和单元格A18中均输入“浙江福建”,注意“浙江”与“福建”中间可用Alt键+Enter键进行强制分行,如图9-24所示。
单击单元格C18,输入“=MAX(C7,C8)”,在区域C18:P18中复制公式;单击单元格Q4,输入“=MAX(F4,G4)”,在区域Q4:Q17中复制公式,注意单元格Q18中的距离值为“0”,具体结果如图9-25所示。
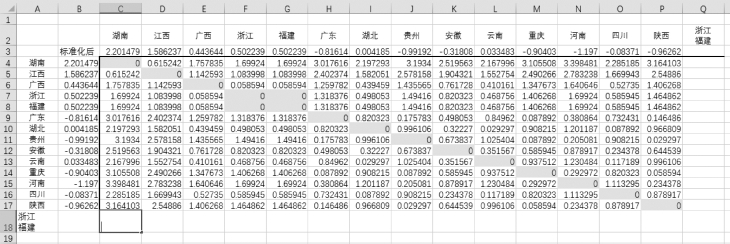
图9-24 “浙江”与“福建”合并成新类
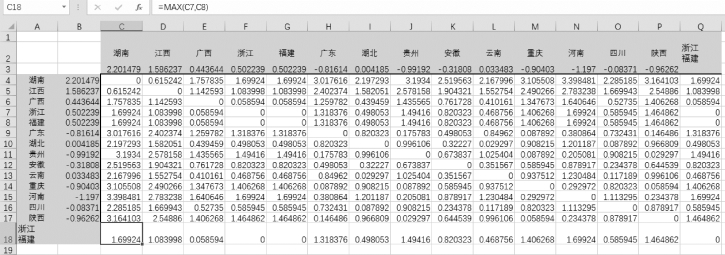
图9-25 用最长距离法计算“浙江、福建”类与其他类的距离
(6)将区域C18:P18和P4:P17中的公式复制粘贴为数据,然后删除浙江和福建的数据行与列,即第8、9行和F、G列,如图9-26所示。
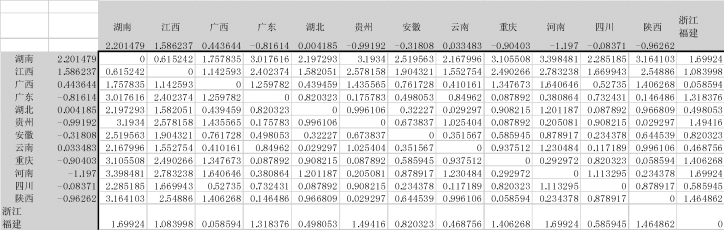
图9-26 删除“浙江”与“福建”类所在的行与列
(7)重复步骤(5)和(6),注意每一次在条件格式中单击后N项,N=实际类数+1,例如在图9-27中有13类,那么N=14(如图9-27~图9~35所示)。将距离最小的两个不同类进行合并,并利用最大距离计算新类的值,直到最后只剩下四类。
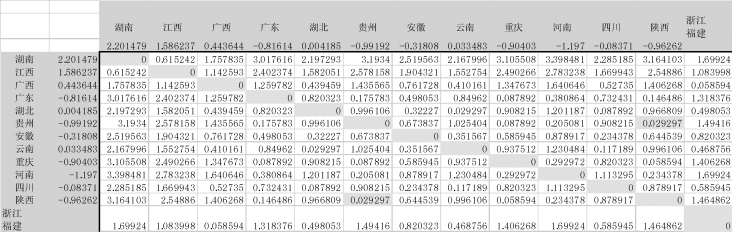
图9-27 利用条件格式选出最小距离的两类“贵州”与“陕西”
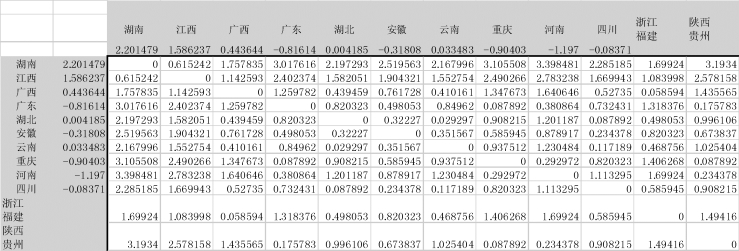
图9-28 将“陕西”与“贵州”合并成新类
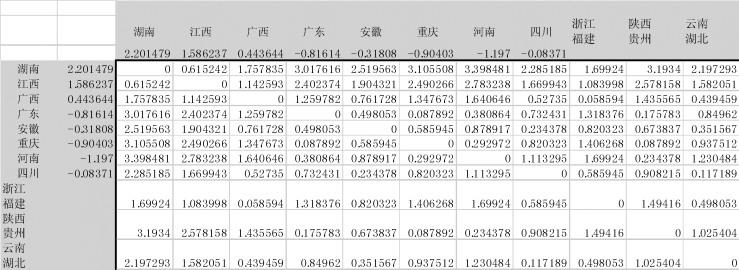
图9-29 将“云南”与“湖北”合并成新类
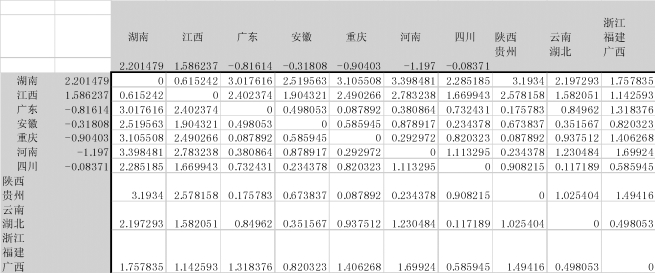
图9-30 将“浙江、福建”与“广西”合并成新类
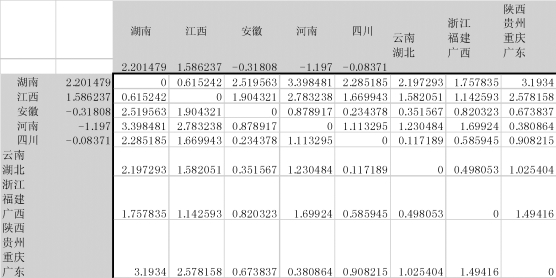
图9-31 将“陕西、贵州、重庆”与“广东”合并成新类
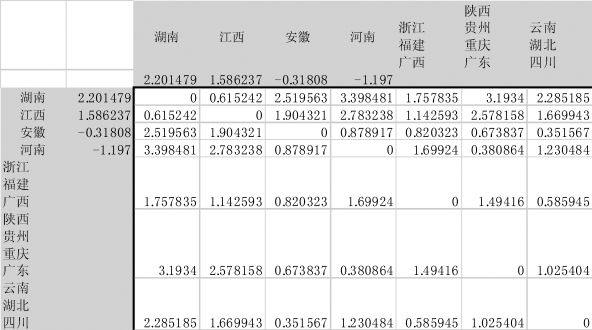
图9-32 将“云南、湖北”与“四川”合并成新类
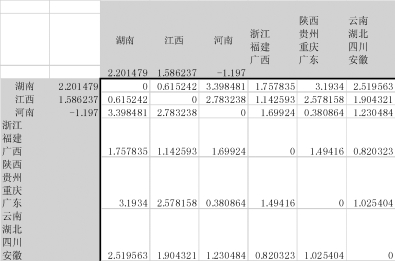
图9-33 将“云南、湖北、四川”与“安徽”合并成新类
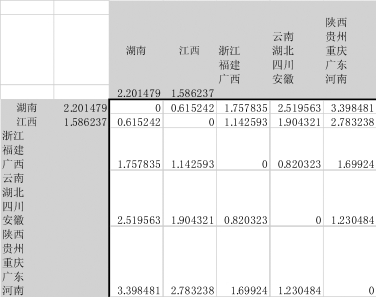
图9-34 将“陕西、贵州、重庆、广东”与“河南”合并成新类
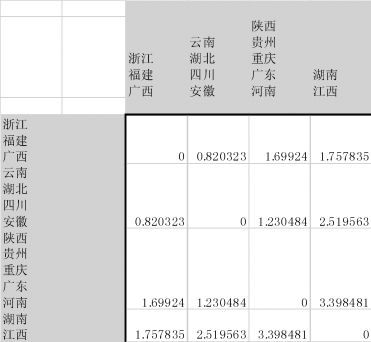
图9-35 将“湖南”与“江西”合并成新类
【结论】油茶产地分布范围最终分为4类,再根据原始数值很容易推断出油茶产地分布的分类,如表9-3所示。
表9-3 油茶产地分布分类

图谱分析如图9-36所示。
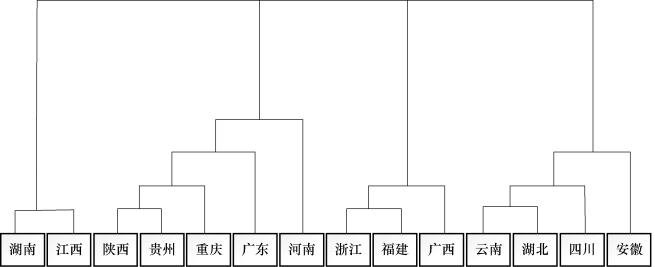
图9-36 最长距离法油茶产地分布图谱分析
聚类分析中的举例分析法是常用的一种方法,然而聚类分析的结果具有不确定性,因为它可能本就没有正确答案,不同的方案会导致不同的分类结果。最短距离法产生的聚类可能会破坏类的“紧凑性”,而最长距离法产生的聚类有可能会破坏类的“闭合性”,也就是分配到某类的样本到其他类成员的距离比本类中的某些成员的距离更短。
在聚类分析的距离分析法中,距离测量方式的选择非常重要,由例9.1和例9.2可以看到,新类的距离测量方式不一样,分类结果也不一样。因为在进行聚类分析的举例分析法时,必须针对样本的具体特征,与实际问题对照,看哪一个结果更符合经验,由此选择合理的距离测量方式与算法,提高聚类的准确性。
关于聚类分析也有一些分类方面的建议。
建议A:任何类都必须在邻近各级中是突出的,即各类重心之间的距离必须为极大。
建议B:确定的类中,两类包含的元素都不过分多。
建议C:分类的数目必须符合实用目的。
建议D:若采用几种聚类方法,则在各自的聚类图中应发现相同的类。
由这些建议,例9.1和例9.2中,最长距离法的分类结果可能比最短距离法的分类结果更合理。
