7.1.1 线性相关分析
线性相关中相关关系的判断主要就是计算相关系数的大小,然后根据相关系数的大小判断两个变量之间的相关关系。Excel 2019提供了相关函数和相关工具可以对相关系数进行方便的计算。
1.相关函数法(CORREL函数)
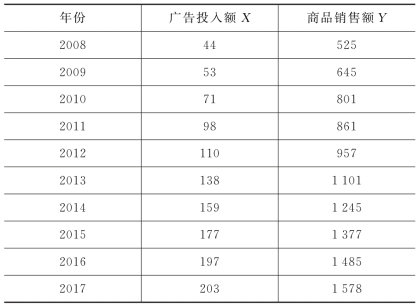
例7.1 某公司统计了2008—2017年公司的广告投入与商品销售额的数据,具体数据如表7-2所示,试确定广告投入与商品销售额的相关关系。
表7-2 某公司广告投入与商品销售额(单位:万元)
【相关函数法分析步骤】
(1)将数据录入Excel表中,如图7-1所示。
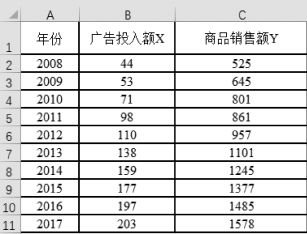
图7-1 按列录入数据
(2)在相关系数对应的单元格输入“=CORREL(B2:B11,C2:C11)”,如图7-2所示。
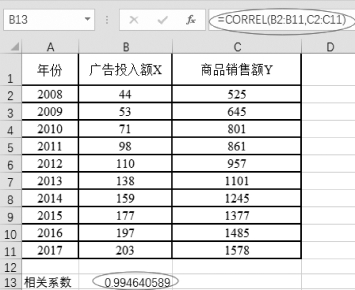
图7-2 计算广告投入与商品销售额的相关系数
CORREL函数返回array1和array2单元格区域的相关系数。其语法为
CORREL(ar ray1,ar ray2)
CORRE函数语法具有下列参数:
•array1:必需,值的单元格区域。
•array2:必需,值的第二个单元格区域。
注意:
(1)如果数组或引用参数包含文本、逻辑值或空白单元格,则这些值将被忽略;但包含零值的单元格将计算在内。
(2)如果array1和array2的数据点的数量不同,函数CORREL返回错误值#N/A。
(3)如果array1或array2为空,或者其数值的s(标准偏差)等于零,函数CORREL返回错误值#DIV/0!。
【结论】
相关系数返回值为0.994 6,因此可以得到出结论:广告投入额和商品销售额具有显著性相关关系。
2.相关分析工具(https://www.daowen.com)
除了使用相关函数以外,Excel的分析工具还给出了相关系数宏工具,相关系数宏工具不但可以求简单相关的相关系数,还可以直接给出多元相关的相关系数矩阵。
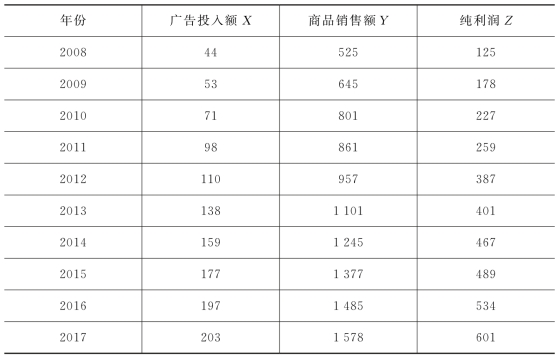
例7.2 某公司统计了2008—2017年公司的广告投入、商品销售额以及纯利润数据,具体如表7-3所示,试确定广告投入、商品销售额与纯利润的相关关系。
表7-3 某公司广告投入、商品销售额与纯利润数据(单位:万元)
【相关函数法分析步骤】
(1)将数据录入Excel表中,如图7-3所示。
(2)选择“数据”选项卡,然后单击“分析”组的“数据分析”工具中的“相关系数”,如图7-4所示。
(3)设置“相关系数”参数,如图7-5所示。
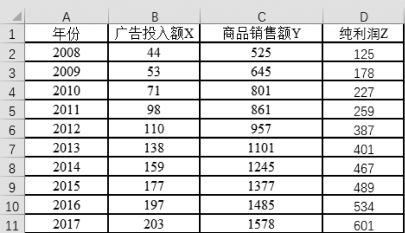
图7-3 按列录入数据
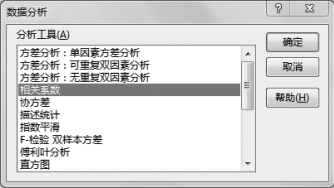
图7-4 数据分析工具中的相关系数
•输入区域:$B$1:$D$11,单击实际数据区域。
•分组方式:逐列,根据实际数据是按照行或列录入单击。
•标志位于第一行:√,根据输入区域是否包含标题行单击。
•输出区域:$A$13。这里可自行单击。
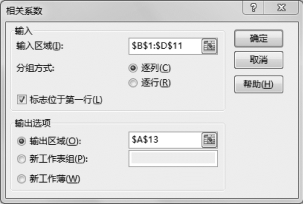
图7-5 相关系数参数设置
(4)相关系数分析结果如图7-6所示。

图7-6 相关系数分析结果
【结论】
广告投入额与商品销售额的相关系数为0.994 6,广告投入额与纯利润的相关系数为0.984 5,商品销售额和纯利润之间的相关系数是0.985 5,因此可以得到出结论:广告投入额、商品销售额和纯利润之间具有显著性相关关系。
