5.3 两个总体方差的F-检验
假设来自正态总体N(μ1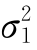
)的样本X 1,X 2,…,X n1和来自正态总体N(μ2
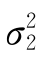)的样本Y 1,Y 2,…,Y n2两样本独立。其样本方差为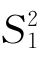
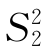。若μ1、μ2
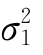和
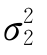均为未知。
现在需要检验假设(显著性水平为α)
那么检验问题的拒绝域为
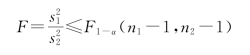
和
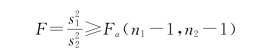
如果需要检验假设(显著性水平为α)
那么检验问题的拒绝域为
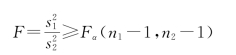
如果需要检验假设(显著性水平为α)
那么检验问题的拒绝域为
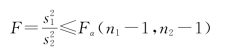
这个检验法就是F-检验法。
“F-检验 双样本方差”分析工具通过双样本F-检验对两个样本总体的方差进行比较。该工具提供的检验结果是以零假设为条件,即两个样本来自具有相同方差的分布,而不是以基础分布中方差不相等的备择假设为条件。
该工具计算F-统计(或F-比值)的f值。接近1的f值证明基础样本总体方差相等。在输出表格中,如果f＜1,“P(F＜=f)单尾”返回当样本总体方差相等时观测到F-统计值小于f的概率,而“F单尾临界值”返回选定显著性水平(Alpha)的小于1的临界值。如果f＞1,“P(F＜=f)单尾”返回当样本总体方差相等时观测到F-统计值大于f的概率,而“F单尾临界值”提供Alpha大于1的临界值。简单地说,F＜F临界,表明两组数据没有显著差异;F≥F临界,表明两组数据存在显著差异。
例5.6 某厂家从两个供货商处进货,分别是货物A和货物B。已经列出两种货物的样本数据,如下所示。
货物A:99,138,88,127,132,88,115,150,114,126,144,148,150,137,139,125,104,132,87,142,146,111,154,103,110,137,111,119,107,151,155,93,113,123,123,95,99,138,115,135,138,130,93,149,135,109,105,133,149,107
货物B:96,132,149,84,114,84,90,97,114,127,128,118,123,127,122,99,113,125,150,94,148,140,96,130,82,100,131,84,80,140,128,127,148,86,122,132,82,91,122,142
试在0.05的显著性水平下运用“F-检验 双样本方差”工具判断货物A的技术指标波动是否明显不同于货物B。
【F-检验步骤】
(1)首先把数据按照“列”的方式排列,如图5-21所示。
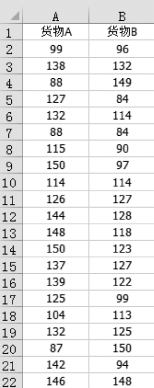
图5-21 按列输入数据
(2)选择“数据”选项卡,然后单击“分析”组的“数据分析”工具中的“F-检验:双样本方差分析”。
(3)设置“F-检验:双样本方差”对话框中的参数,如图5-22所示。
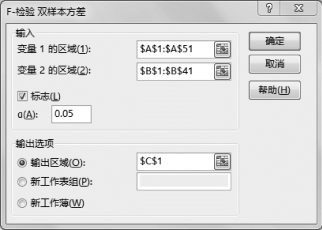
图5-22 “F-检验:双样本方差”分析参数
•输入变量1的区域:$A$1:$A$51,选中变量1的数据区域。
•输入变量2的区域:$B$1:$B$41,选中变量2的数据区域。
•标志:√,如果变量区域选中了标题行,则单击,否则不单击。
•输出区域:$C$1(可自行单击)
(4)得到“F-检验:双样本方差”分析结果,如图5-23所示。
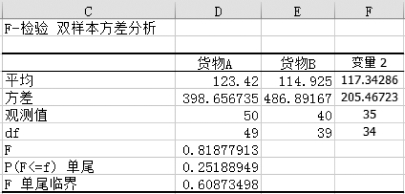
图5-23 “F-检验:双样本方差”分析结果
结论中,因为F=0.818 8＜1,“P(F＜=f)单尾”返回当样本总体方差相等时观测到F-统计值小于f的概率为0.25,而“F单尾临界值”返回选定显著性水平(0.05)的小于1的临界值为0.608 7。
(5)因为“P(F＜=f)单尾”的值0.25＞0.05,所以得到结论:在0.05的显著性水平下,不拒绝
因为F=0.818 8＞0.608 7,所以得到结论:在0.05的显著性水平下,不拒绝