5.4.1 已知标准差的两个正态总体均值之差的临界值法与P值法假设检验
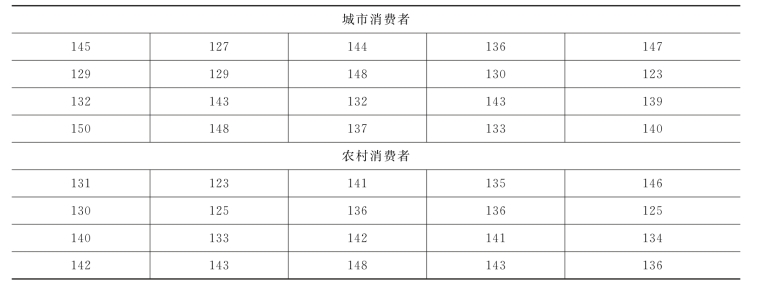
例5.7 某公司为了分析公司产品的销售情况,调查城市消费者和农村消费者在消费上是否存在差别。已知两地消费者的消费均服从正态分布,且城市消费者消费标准差为10,农村消费者消费标准差为7。调查公司从两地客户的电话缴费单中随机各抽取20名,统计消费的结果如表5-6所示,试在0.05的显著性水平下判断两地客户之间是否存在差别。
表5-6 城市与农村消费者电话缴费单
【临界值法步骤】
按照题意检验假设
H 0:μ1=μ2;H 1:μ1≠μ2
解答过程如下:
(1)单击单元格B16,计算平均值为“=AVERAGE(A1:E5)”,结果为137.75。
(2)单击单元格D16,计算平均值为“=AVERAGE(A7:E10)”,结果为136.50,如图5-24所示。
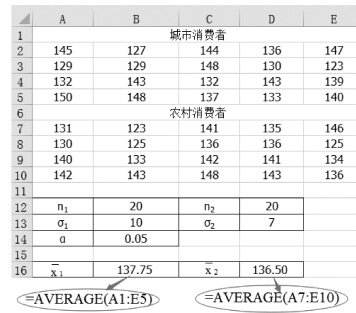
图5-24 城市与农村消费者均值
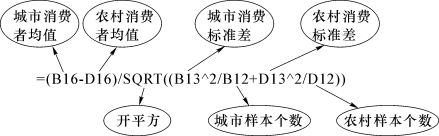
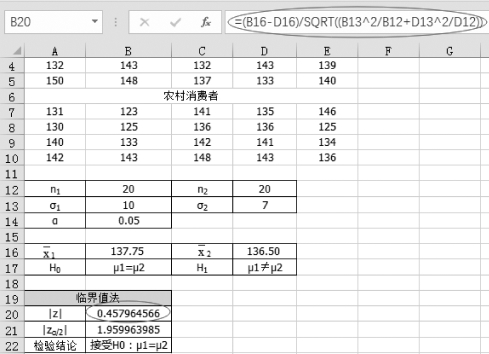
(3)单击单元格B20计算z值,输入“=(B16-D16)/SQRT((B13 2/B12+D13 2/D12))”。
函数解析:
结果为0.458 0,如图5-25所示。
图5-25 均值差的统计量
(4)单击单元格B21计算临界值,输入“=ABS(NORM.S.INV(B14/2))”,结果为1.96,如图5-26所示。
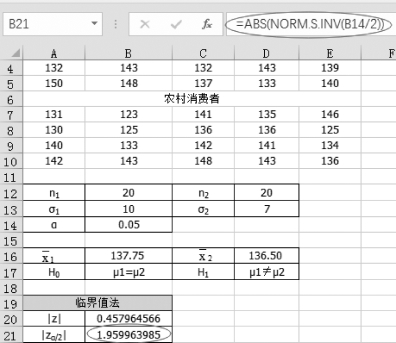
图5-26 均值差的临界值
(5)单击单元格B22得到结论,输入“=IF(B20＜B21,"接受H0:μ1=μ2","接受H1:μ1≠μ2")”,如图5-27所示。
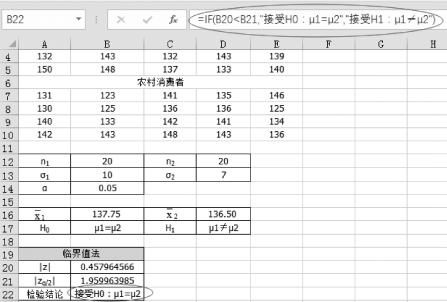
图5-27 临界值法的结论
【P值法步骤】
(1)单击单元格B25,输入“=1-NORM.S.DIST(B20,1)”,结果为0.323 5,如图5-28所示。
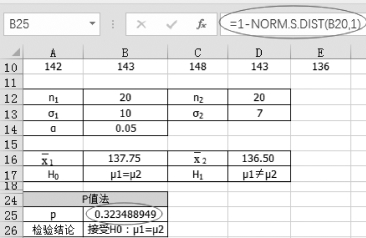
图5-28 统计量对应的概率
(2)单击单元格B26,输入“=IF(B25＞B14/2,"接受H0:μ1=μ2","接受H1:μ1≠μ2")”,得到结论,如图5-29所示。
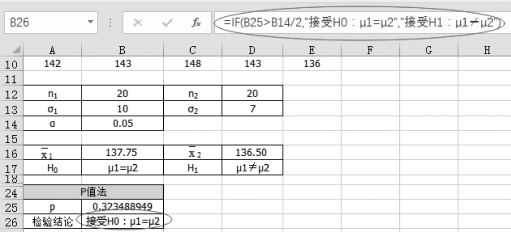
图5-29 P值法的结论
【结论】
无论是临界值法还是P值法,都得到相同的结论:在0.05的显著性水平下,判断农村消费者和城市消费者之间不存在显著性差异。