2.1.2 泊松分布
泊松分布主要用来描述某时段时间内随机事件发生不同次数的概率,对应的概率分布为
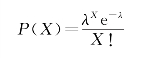
概率分布函数为
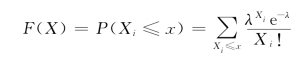
期望与方差为
![]()
具有泊松分布的随机变量在实际应用中是很多的。例如,某一服务设施在一定时间内到达的人数、电话交换机接到呼叫的次数、汽车站台的候车人数、机器出现的故障数、自然灾害发生的次数、一块产品上的缺陷数、显微镜下单位分区内的细菌分布数等。
Excel 2019提供的泊松分布函数为POISSON.DIST函数。
POISSON.DIST函数返回泊松分布的概率。
POISSON.DIST函数语法:
POISSON.DIST(x,mean,cumulat ive)
POISSON.DIST函数语法具有下列参数:
•x:必需,事件数。(https://www.daowen.com)
•mean:必需,期望值。
•cumulative:必需,逻辑值,确定所返回的概率分布的形式。
✧如果cumulative为TRUE(1),则POISSON.DIST返回发生的随机事件数在0(含0)和x(含x)之间的累积泊松概率;
✧如果cumulative为FALSE(0),则POISSON返回发生的事件数正好是x的泊松概率密度函数。
注意:在以前的版本中,POISSON函数返回泊松分布,此函数已被替换为POISSON.DIST,POISSON.DIST函数可提供更高的精确度,其名称更好地反映其用法。虽然POISSON函数仍可向后兼容,但仍应该考虑从现在开始使用新函数,因为此函数在Excel的将来版本中可能不再可用。
例2.3 某公共汽车站早上9点到10点的候车人数符合泊松分布,已知这一时间段平均候车人数为63人,那么今天该汽车站早上9点到10点的候车人数为55人的概率是多少?今天该汽车站早上9点到10点的候车人数低于55人的概率是多少?
【实验步骤】
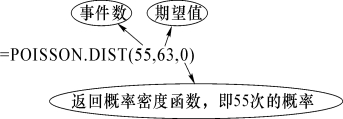
(1)在选中单元格中输入“=POISSON.DIST(55,63,0)”,显示结果为0.032,即该汽车站今天早上9点到10点的候车人数为55人的概率是0.032。
POISSON概率密度函数解析:
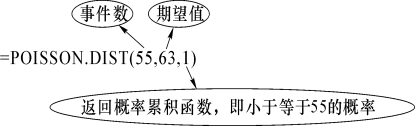
(2)在选中单元格中输入“=POISSON.DIST(55,63,1)”,显示结果为0.173,即该汽车站今天早上9点到10点的候车人数少于55人的概率是0.173。
POISSON.DIST概率累积函数解析: