8.3.1　中心移动平均

8.3.1　中心移动平均

中心移动平均法是将时间序列变量值以当前时间数据为中心做K项的滚动平均。

对于时间序列A 1,A 2,…,A n,对应中心移动平均法进行平均结果如下。

当移动平均时距项数K为奇数时,以当前时间数据A t为中心,要求K项的平均,那么只需要进行一次平均即可。

而当移动平均项数K为偶数时,当前时间数据A t就不在中心位置了,因此需要再进行一次相邻两项平均值的移动平均,才能使二次平均值的中心正好对着某一时期值。这个过程也被称为移正平均,使得二次平均值也成为中心化的移动平均数。

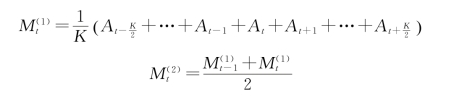
这里t为

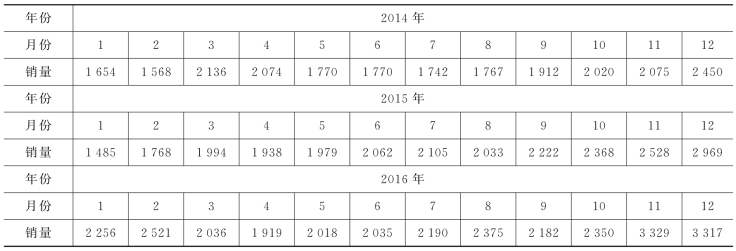
例8.2 已知某企业连续3年的销量(单位:件)如表8-6所示,试用平均项数12的中心移动平均法研究该企业销量的变化趋势。

表8-6　某企业连续3年的销量表

【中心移动平均】

(1)将表中所有数据按列录入工作表内,如图8-1所示。

(2)计算一次平均,也就是每12个销量的滚动平均。在单元格C7中输入“=AVERAGE(B2:B13)”,然后向下复制公式至单元格C31,如图8-2所示。

注意:第一项一次移动平均是2014年1月到12月的平均值,最后一项一次移动平均值是2016年1月到12月的平均值。

(3)计算二次平均,也就是每两个一次平均值的滚动平均值。即在单元格D8中输入“=AVERAGE(C7:C8)”,然后向下复制公式至单元格D31,如图8-3所示。

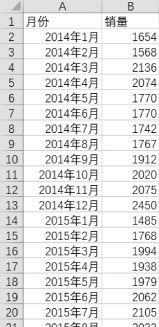
图8-1　按列录入工作表

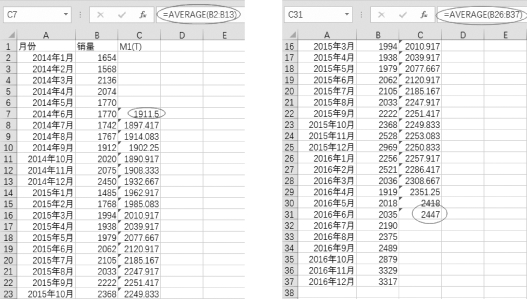
图8-2　计算12项一次平均值

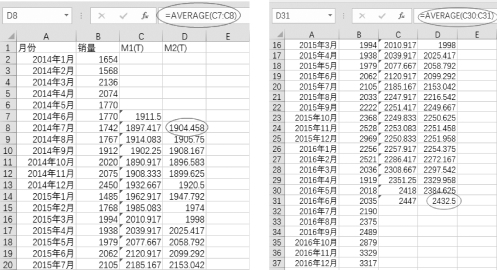
图8-3　计算12项二次平均值

(4)绘制销量的散点图与中心移动平均的折线图,如图8-4所示。

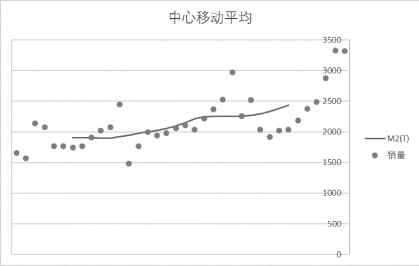
图8-4　中心移动平均折线图