7.2.3 利用回归工具建立多元线性回归方程
Excel 2019提供的回归工具不仅可以建立一元线性回归方程,还可以利用该工具对多个自变量进行分析,建立多元线性回归方程。
例7.7 已知某企业分析了该企业近15年来的年销售收入,认为影响销售收入的主要因素是销售人员数量、年广告费用和固定投资额度,其原始数据(单位:万元)如表7-6所示。
表7-6 某企业销售收入、销售人员数量、年广告费用与固定投资额度数据
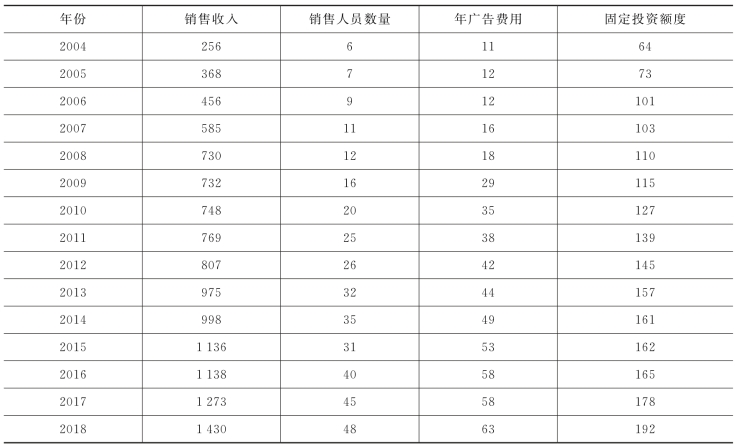
利用Excel对该企业的年销售收入、销售人员数量、年广告费用和固定投资额度进行回归分析。
【回归工具步骤】
假设销售收入为A,销售人员数量为x,年广告费用为y,固定投资额度为z。
(1)将数据录入Excel表中,如图7-29所示。
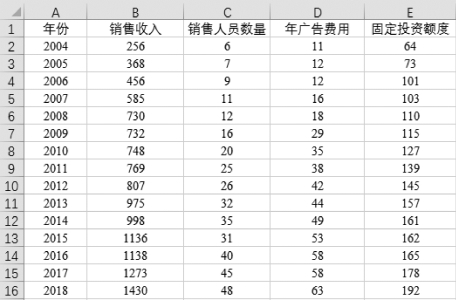
图7-29 按列录入数据
(2)选择“数据”选项卡,然后单击“分析”组的“数据分析”工具中的“回归”,如图7-30所示。
图7-30 选择回归工具
(3)设置“回归”参数,如图7-31所示。
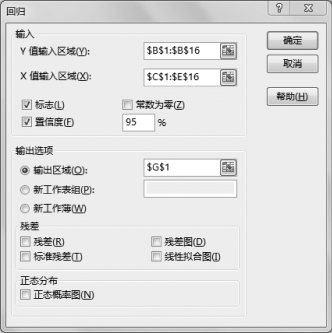
图7-31 设置回归工具参数
•Y值输入区域:$B$2:$B$16,单击实际数据区域。
•X值输入区域:$C$1:$E$16,单击实际数据区域。
•标志:√,根据输入区域是否包含标题行单击。
•置信度:95%,根据实验要求输入。
•输出区域:$G$1。这里可自行单击。
(4)回归分析结果如图7-32所示。
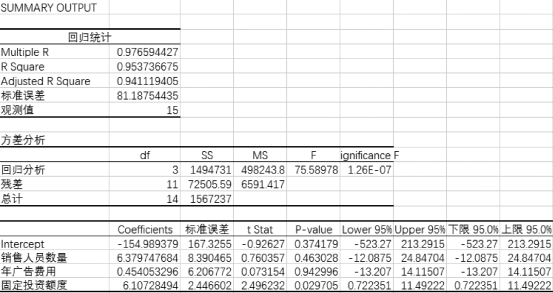
图7-32 回归分析结果
【结论】
(1)根据回归统计表可以得到相关系数为0.976 594 427,说明销售人员数量、年广告费用、固定投资额度与销售收入显著性相关,呈线性正相关关系。
(2)根据回归统计表可以得到估计的标准误差为81.187 544 35。
(3)根据回归统计表可以得到R 2=0.953 736 675,表明总误差平方和中有95.37%可以由回归方程来解释。
(4)根据回归的汇总输出可以得到线性回归方程为
A=6.38x+0.45y+6.11z-155
(5)Intercept对应的P值为0.374＞0.05,表明该常数项对回归方程的影响统计上不显著。
(6)“销售人员数量”对应的P值为0.463＞0.05,表明该常数项对回归方程的影响统计上不显著。
(7)“广告费用”对应的P值为0.943＞0.05,表明该常数项对回归方程的影响统计上不显著。
(8)“固定投资额”对应的P值为0.030＜0.05,表明该常数项对回归方程的影响显著,即在以上三个自变量中,只有“固定投资额”变量在统计上起到显著性作用。