2.1.1 二项分布与二项分布函数
设随机变量X只可能取0与1两个值,它的分布律是
P{X=0}=1-p, P{X=1}=p
其中0＜p＜1,则称X服从以p为参数的(0,1)分布或两点分布。
(0,1)分布的分布律也可写成表2-2所示的形式。
表2-2 (0,1)分布
假设实验E只有两个可能的结果:A和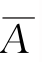
,则称E为伯努利(Bernoulli)实验。那么
其中0＜p＜1。将E独立重复地进行n次,则称这一串重复的独立实验为n重伯努利实验。
这里“独立”是指在每次实验中P(A)=p保持不变,每次实验的结果互不影响。n重伯努利实验是一种很重要的数学模型,它有广泛的应用,是研究得最多的模型之一。
以X表示n重伯努利实验中事件A发生的次数,X是一个随机变量,X的分布律为
记q=1-p,那么
X的数学期望为μ=np,方差为σ2=np(1-p)。
Excel 2019中有三个二项分布相关函数,可以用来计算二项分布的概率与反函数值。
1.BINOM.DIST函数
BINOM.DIST函数返回一元二项式分布的概率,用于处理固定次数的实验或实验问题,前提是任意实验的结果仅为成功或失败两种情况,实验是独立实验,且在整个实验过程中成功的概率固定不变。例如,BINOM.DIST可以计算三个即将出生的婴儿中两个是男孩的概率。
BINOM.DIST函数语法:
BINOM.DIST(number_s,t r ial s,probability_s,cumulat ive)
其中参数表示:
•number_s:必需,实验的成功次数。
•trials:必需,独立实验次数。
•probability_s:必需,每次实验成功的概率。
•cumulative:必需,决定函数形式的逻辑值。
✧如果cumulative为TRUE(1),则BINOM.DIST返回累积分布函数,即最多存在number_s次成功的概率;
✧如果cumulative为FALSE(0),则返回概率密度函数,即存在number_s次成功的概率。
注意:
①二项式概率密度函数为
累积二项式分布函数的公式为
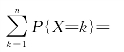
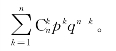
②Excel在以前的版本中提供的一元二项式分布函数为BINOMDIST,虽然此函数仍可向后兼容,但大家应该考虑从现在开始使用新函数,因为BINOMDIST函数在Excel的将来版本中可能不再可用。
例2.1 一张考卷上有5道选择题,每道题列出4个可能的答案,其中只有一个答案是正确的。某学生靠猜测至少能答对4道题的概率是多少?
【方法1】使用BINOM.DIST概率函数
①在单元格A1中输入“=BINOM.DIST(4,5,0.25,0)”,返回答对4道题的概率。
BINOM.DIST概率密度函数解析:
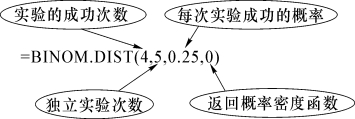
②在单元格B1中输入“=BINOM.DIST(5,5,0.25,0)”,返回答对5道题的概率。
③在单元格C1中输入“=A1+B1”,返回答对4道题与5道题的概率之后,结果显示为0.015 625。
【方法2】使用BINOM.DIST概率累积函数
在单元格A2中输入“=1-BINOM.DIST(3,5,0.25,1)”,结果显示为0.015 625。
BINOM.DIST概率累积函数解析:
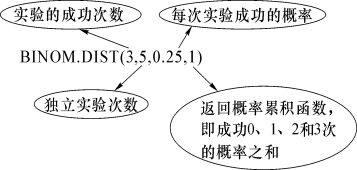
这里BINOM.DIST(3,5,0.25,1)表示最多答对3次的概率累积函数,所有情况的概率之和为1,所以1-BINOM.DIST(3,5,0.25,1)表示去掉答对0、1、2和3次成功的概率,剩下的就是至少答对4次的概率。
2.BINOM.DIST.RANGE函数
BINOM.DIST.RANGE函数使用二项式分布返回实验结果的概率,也能返回在指定成功次数之间的概率。
BINOM.DIST.RANGE函数语法:
BINOM.DIST.RANGE(t r ial s,probability_s,number_s,[number_s2])
其中参数表示:
•trials:必需,独立实验次数,必须大于或等于0。
•probability_s:必需,每次实验成功的概率,必须大于或等于0并小于或等于1。
•number_s:必需,实验成功次数,必须大于或等于0并小于或等于trials。
•number_s2:可选,如提供,则返回实验成功次数将介于number_s和number_s2之间的概率,必须大于或等于number_s并小于或等于trials。
下面仍然以例2.1为例。
【方法3】使用BINOM.DIST.RANGE函数,如图2-1所示。
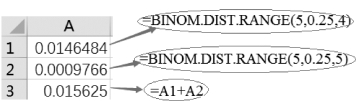
图2-1 BINOM.DIST.RANGE函数的使用
①在单元格A1中输入“=BINOM.DIST.RANGE(5,0.25,4)”,返回答对4道题的概率,结果为0.014 648。
②在单元格A2中输入“=BINOM.DIST.RANGE(5,0.25,5)”,返回答对5道题的概率,结果为0.000 977。
③在单元格A3中输入“=A1+A2”,返回答对4道题与5道题的概率之后,结果显示为0.015 625。
注意:在方法3中BINOM.DIST.RANGE函数第4个参数缺省,此处BINOM.DIST.RANGE函数的功能等同于方法1中的BINOM.DIST概率密度函数。
【方法4】使用BINOM.DIST.RANGE函数的范围
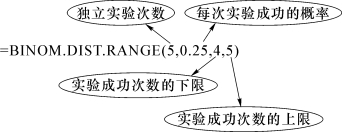
在单元格A2中输入“=BINOM.DIST.RANGE(5,0.25,4,5)”,结果显示为0.015 625。
BINOM.DIST.RANGE函数解析:
3.BINOM.INV函数
BINOM.INV函数返回一个数值,它是使得累积二项式分布的函数值大于等于临界值的最小整数。
BINOM.INV函数语法:
BINOM.INV(t r ials,probability_s,alpha)
BINOM.INV函数语法具有以下参数:
•trials:必需,伯努利实验次数。
•probability_s:必需,一次实验中成功的概率。
•alpha:必需,临界值。
注意:在以前的版本中,CRITBINOM函数返回一个数值,它是使得累积二项式分布的函数值大于等于临界值的最小整数。但是现在CRITBINOM函数已被替换为BINOM.INV函数,BINOM.INV函数可提供更高的精确度,其名称更好地反映其用法。虽然CRITBINOM函数仍可向后兼容,但我们仍应该考虑从现在开始使用新函数,因为此函数在Excel的将来版本中可能不再可用。
仍然以例2.1为例,那么“=BINOM.INV(5,0.25,0.75)”显示的结果为2,所表示的实际意义是,5道选择题正确率为0.25,那么75%的可能性答对2道题。
例2.2 某种产品使用寿命超过10 000小时的为合格品。已知一只该产品合格的概率为0.72,从中随机抽取50只产品,为了保证90%的合格率,那么抽取的50只产品中至少需要包含几只合格品?
【实验步骤】
在选中单元格中输入“=BINOM.INV(50,0.72,0.9)”,显示结果为40。
BINOM.INV函数解析:
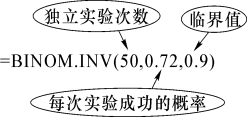
即在抽取的50只产品中,如果至少有40只合格品,就能保证合格率达到90%。