2.2.2 标准正态分布
标准正态分布又称为U分布,是以0为均数、以1为标准差的正态分布,记为N(0,1)。
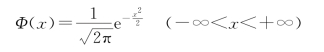
标准正态分布曲线下面积分布规律是:在-1.96~+1.96范围内曲线下的面积等于0.950 0,在-2.58~+2.58范围内曲线下面积为0.990 0。统计学家还制定了一张统计用表(自由度为∞时),借助图2-3就可以估计出某些特殊μ1和μ2值范围内的曲线下面积。
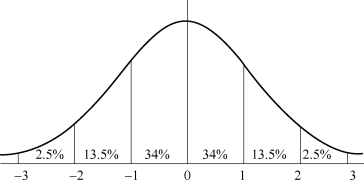
图2-3 标准正态分布规律
一般来说,如果正态分布X~N(μ,σ2),那么可以通过一个线性变换的标准化操作将正态分布化成标准正态分布,如图2-4所示。
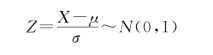
根据“3σ”法则,标准正态分布满足:
•函数曲线下68.268 949%的面积在(-1,1)范围内。
•函数曲线下95.449 974%的面积在(-2,2)范围内。
•函数曲线下99.730 020%的面积在(-3,3)范围内。
•函数曲线下99.993 666%的面积在(-4,4)范围内。
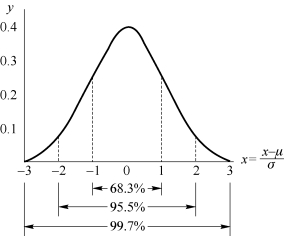
图2-4 转化为标准正态分布
Excel 2019为标准正态分布提供了两个函数。
1.NORM.S.DIST函数
NORM.S.DIST函数返回标准正态分布函数,可以使用此函数代替标准正态曲线面积表。
NORM.S.DIST函数语法:
NORM.S.DIST(z,cumulative)
NORM.S.DIST函数语法具有下列参数:
•z:必需,需要计算其分布的数值。
•cumulative:必需,cumulative是决定函数形式的逻辑值。
✧如果cumulative为TRUE(1),则返回累积分布函数;
✧如果cumulative为FALSE(0),则返回概率密度函数。
2.NORM.S.INV函数
NORM.S.INV函数返回标准正态累积分布函数的反函数值。该分布的平均值为0,标准偏差为1。(https://www.daowen.com)
NORM.S.INV函数语法:
NORM.S.INV(probability)
NORM.S.INV函数的参数probability是必需的,对应于正态分布的概率。
备注:
①如果已给定概率值,则NORM.S.INV使用NORM.S.DIST(z,TRUE)=probability求解数值z。因此,NORM.S.INV的精度取决于NORM.S.DIST的精度。NORM.S.INV使用迭代搜索技术。
②Excel提供的早期正态分布函数的反函数值为NORMSINV(probability)。
例2.5 随机选择某些数值,分别计算这些数值的正态分布累积概率,然后反求这些数值。
【实验步骤】
(1)在单元格A1:C1中分别输入“随机数”、“标准正态分布累积函数”和“反求数值”。
(2)选择“数据”选项卡“分析”组的“数据分析”命令,在对话框中选择“随机数发生器”,如图2-5所示。
(3)在“随机数发生器”对话框中选择合适的参数,如图2-6所示。
图2-5 随机数发生器
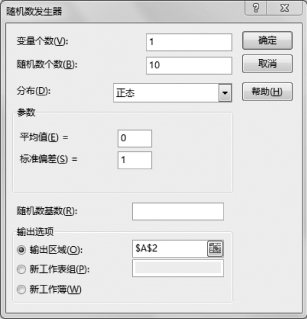
图2-6 “随机数发生器”对话框
•变量个数:1;
•随机数个数:10;
•分布:正态;
•平均值:0;
•标准偏差:1;
•输出区域:A2。
单击“确定”按钮后,生成10个满足正态分布的随机数。
(4)选中单元格B2,输入“=NORM.S.DIST(A2,1)”,在B3:B11区域中复制该公式。
(5)选中单元格C2,输入“=NORM.S.INV(B2)”,在C3:C11区域中复制该公式。最终结果如图2-7所示。
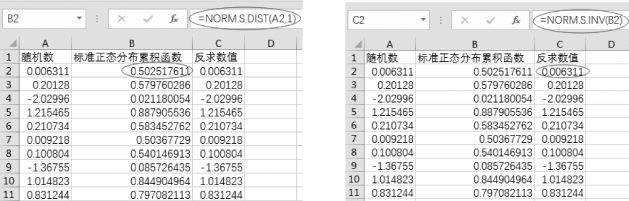
图2-7 标准正态分布累积函数与反求数值
