2.4.2 标准差与方差函数
方差与标准差都是用来描述数据离散程度的,标准差在方差基础上多了个根号。由于标准差和均值的量纲(单位)是一致的,在描述一个波动范围时标准差比方差更方便,比如一个班男生的平均身高是170 cm,标准差是10 cm,那么方差就是100 cm2。可以进行的比较简便的描述是本班男生身高分布是(170±10)cm,方差就无法做到这点。因此,在Excel实验中使用标准差要更多,大家在实验的时候务必注意到方差与标准差的区别。
Excel 2019为标准差和方差分别提供了两个函数,即样本标准差(方差)函数和总体标准差(方差)函数。
1.标准差
(1)样本标准差STDEV.S函数
STDEV.S函数是基于样本估算标准偏差(忽略样本中的逻辑值和文本),标准偏差可以测量值在平均值附近分布的范围大小。STDEV.S函数的计算公式如下:
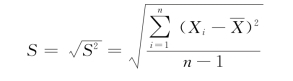
STDEV.S函数语法:
STDEV.S(number1,[number2],...)STDEV.P(number1,[number2],...)
STDEV.S函数语法具有下列参数:
•number1:必需,对应于总体样本的第一个数值参数。也可以用单一数组或对某个数组的引用来代替用逗号分隔的参数。
•number2,...:可选,对应于总体样本的2~254个数值参数。也可以用单一数组或对某个数组的引用来代替用逗号分隔的参数。
注意:STDEV.S函数假设其参数是总体样本。如果数据代表整个总体,请使用STDEV.P计算标准偏差。
(2)总体标准差STDEV.P函数
STDEV.P函数计算基于以参数形式给出的整个样本总体的标准偏差(忽略逻辑值和文本),标准偏差可以测量值在平均值(中值)附近分布的范围大小。STDEV.P函数的计算公式如下:
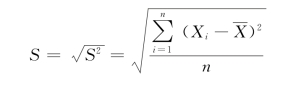
STDEV.P函数语法:
STDEV.P函数语法具有下列参数:
•number1:必需,对应于总体的第一个数值参数。
•number2,...:可选,对应于总体的2~254个数值参数。也可以用单一数组或对某个数组的引用来代替用逗号分隔的参数。
注意:(https://www.daowen.com)
①STDEV.P假定其参数是整个总体。如果数据代表总体样本,请使用STDEV计算标准偏差。
②对于大样本容量,函数STDEV.S和STDEV.P计算结果大致相等。
③如果要使计算包含引用中的逻辑值和代表数字的文本,请使用STDEVPA函数。
另外,Excel早期还提供了STDEV函数、STDEVP函数和STDEVA函数,这些函数已被替换为上述介绍的新函数,新函数可提供更高的精确度,其名称更好地反映其用法。虽然这些函数仍可向后兼容,但在Excel的将来版本中可能不再可用。
2.方差
(1)样本标准差VAR.S函数
VAR.S函数是基于样本方差(忽略样本中的逻辑值和文本)的,VAR.S函数的计算公式如下:
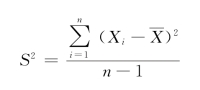
VAR.S函数语法:
VAR.S(number1,[number2],...)VAR.P(number1,[number2],...)
VAR.S函数语法具有下列参数:
•number1:必需,对应于总体样本的第一个数值参数。也可以用单一数组或对某个数组的引用来代替用逗号分隔的参数。
•number2,...:可选,对应于总体样本的2~254个数值参数。也可以用单一数组或对某个数组的引用来代替用逗号分隔的参数。
(2)总体标准差VAR.P函数
VAR.P函数计算基于整个样本总体的方差(忽略逻辑值和文本),VAR.P函数的计算公式如下:
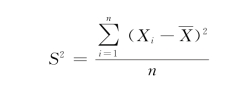
VAR.P函数语法:
VAR.P函数语法具有下列参数:
•number1:必需,对应于总体的第一个数值参数。
•number2,...:对应于总体的2~254个数值参数。也可以用单一数组或对某个数组的引用来代替用逗号分隔的参数。
