8.1 时间序列简介
时间序列由两部分组成:时间和不同时间的具体指标数值,如表8-1所示。
表8-1 时间序列的组成

时间序列的统计解释是某项统计指标按时间顺序记录的指标值数列。时间序列的系统意义是某一系统运行过程中在不同时间点的响应,是系统行为量化数据的有序客观记录,反映了系统的结构特征和运行规律。时间序列的数学实质X 1,X 2,…,X N是按时间次序排列的随机变量序列,其观测值序列x 1,x 2,…,x n称为X 1,X 2,…,X N的一条轨迹或一次实现,轨迹片段x 1,x 2,…,x n称为N个观测样本。时间序列X 1,X 2,…,X N简记为{Xt,t∈T}或X( t)。
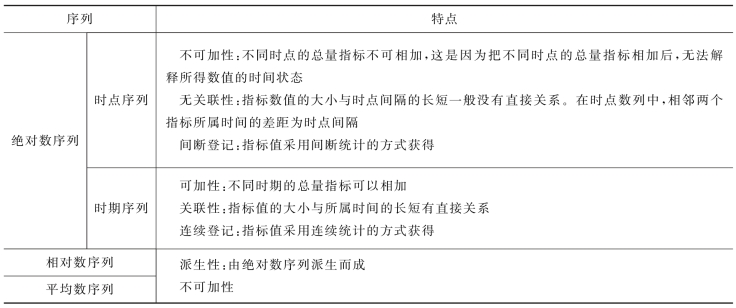
时间序列分为三类:绝对数时间序列、相对数时间序列和平均数时间序列。
1.绝对数时间序列
绝对数时间序列又称从总量指标时间序列,指将一系列同类的统计绝对数按照时间先后顺序排列起来而形成的统计序列。绝对数时间序列反映各时期内的总量水平,或者各时点上的发展水平。
绝对数时间序列又分为以下两类。
(1)时期序列
时期序列是由时期总量指标排列而成的时间序列。它的主要特点为
①序列中的指标数值具有可加性;
②序列中每个指标数值的大小与其所反映的时期长短有直接联系;
③序列中每个指标数值通常是通过连续不断登记汇总取得的。
(2)时点序列
时点序列是由时点总量指标排列而成的时间序列。时点序列中的指标数值不具可加性,序列中每个指标数值的大小与其间隔时间的长短没有直接联系,而且时点序列中每个指标数值通常是通过定期的一次登记取得的。
2.相对数时间序列
相对数时间序列是把一系列同种相对数指标按时间先后顺序排列而成的时间序列,反映社会经济现象数量对比关系的变化情况。
3.平均数时间序列
平均数时间序列是指由一系列同类平均指标按时间先后顺序排列的时间序列,反映社会经济现象一般水平的变化过程。
时间序列的分类与其对应特征如表8-2所示。
表8-2 时间序列的分类
例如,表8-3是某公司2012—2017年职工工资与员工人数统计表。
表8-3 员工统计表

其中职工工资总额是时期序列,年末职工人数为时点序列,男性职工占比为相对数序列,职工平均货币工资为平均数序列。很明显职工工资总额具有可加性,2 990.7+2 747.2=5 737.9万元是2016—2017两年的职工工资总额。而年末职工人数、男性职工占比和职工平均货币工资相加没有实际意义。
时间序列的作用是计算水平指标和速度指标,分析社会经济现象发展过程与结果,并进行动态分析;利用数学模型揭示社会经济现象发展变化的规律性并预测现象未来的发展趋势;揭示现象之间的相互联系程度及其动态演变关系。时间序列分析是定量预测方法之一,它的基本原理是承认事物发展的延续性,同时考虑事物发展的随机性。应用过去数据,就能推测事物的发展趋势,但是任何事物发展都可能受偶然因素影响,为此要利用统计分析中的加权平均法对历史数据进行处理。时间序列分析的方法简单易行,便于掌握,但准确性差,一般只适用于短期预测。时间序列预测一般反映三种实际变化规律:趋势变化、周期性变化、随机性变化。
时间序列的构成因素如下。(https://www.daowen.com)
•长期趋势(T):长期趋势变动又称趋势变动,是时间序列在较长持续期内表现出来的总态势,是由现象内在的根本性、本质因素决定的,支配着现象沿着一个方向持续上升、下降或在原有水平上起伏波动。长期趋势时间序列具有随时间的变化而逐渐增加或减少的长期变化趋势。
•季节变动(S):季节变动时间序列在一年中或固定时间内,呈现出固定规则的变动。
•循环变动(C):循环变动是在时间序列中以若干年为周期、上升与下降交替出现的循环往复的运动。例如经济增长中的商业周期具有“繁荣-衰退-萧条-复苏-繁荣”的循环变动,固定资产或耐用消费品的更新周期等。
•随机变动(R):由于偶然性因素的影响而表现出的不规则波动,故也称为不规则变动。随机变动的成因包括自然灾害、意外事故、政治事件与大量无可言状的随机因素的干扰。
时间序列分析分为加法模型和乘法模型。
•加法模型:假定四种变动因素相互独立,数列各时期发展水平是各构成因素之总和。
Y=T+S+C+I
•乘法模型:假定四种变动因素之间存在着交互作用,数列各时期发展水平是各构成因素之乘积。
Y=T×S×C×I
时间序列的分解分析就是按照时间序列的分析模型,测定出各种变动的具体数值。其分析取决于时间序列的构成因素。
①仅包含趋势变动和随机变动(年度数据):
乘法模型为
Y=T×I
加法模型为
Y=T+I
消除随机变动,测算出长期趋势。
②含趋势、季节和随机变动:
按月(季)编制的时间序列通常具有这种形态。
分析步骤如下。
a.分析和测定趋势变动,求趋势值T。
b.对时间序列进行调整,得出不含趋势变动的时间序列资料。
乘法
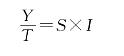
加法
Y-T=(T+S+I) -T=S+I
c.对以上的结果进一步进行分析,消除随机变动I的影响,得出季节变动的测定值S。
时间序列分解分析可以测定各构成因素的数量表现,认识和掌握现象发展的规律。也可以将某一构成因素从数列中分离出来,便于分析其他因素的变动规律,为时间序列的预测奠定基础。对时间序列的长期趋势的测定主要是为了研究现象发展的主要趋势,同时也为通过分解模型研究季节变动或循环变动提供基础。
