5.2　单个正态总体均值的假设检验

5.2　单个正态总体均值的假设检验

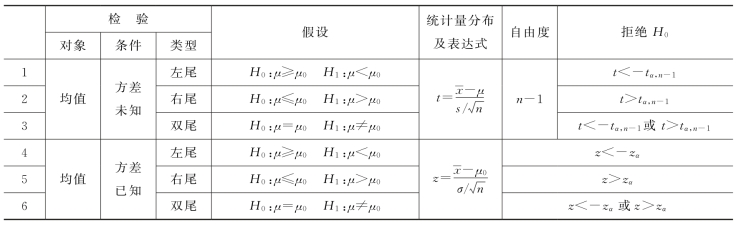
对总体均值的假设而言一般有以下3种情况:

H 0:μ=μ0;H 1:μ≠μ0

H 0:μ≥μ0;H 1:μ＜μ0

H 0:μ≤μ0;H 1:μ＞μ0

当检验H 0:μ=μ0,H 1:μ≠μ0时,需要用到双侧假设检验。这里备择假设H 1:μ≠μ0表示μ可能大于μ0,也可能小于μ0。双侧假设检验的目的是为了观察在给定的显著性水平下所抽取的样本统计量是否显著异于总体参数,如图5-1所示。

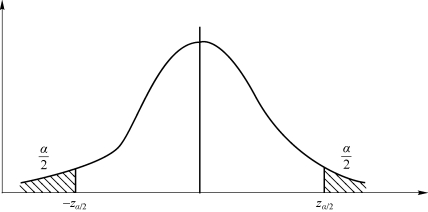
图5 - 1 双侧假设检验

当检验其他两种情况时,需要用到单侧假设检验。单侧假设检验又分为单侧左尾检验和单侧右尾检验。

对于单样本均值的假设检验来说,分为方差已知和方差未知两种情况。

(1)总体服从均值为μ、方差已知为σ2的正态分布时,总体的随机样本均值

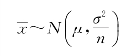
即

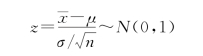
(2)总体的方差无法获知时,可以用能计算出来的样本的标准差S来代替未知的总体的标准差,但是新的统计量不再服从正态分布,而是服从自由度为n-1的t分布:

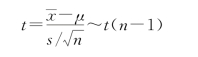
假设检验中的原假设H 0与备择假设H 1在显著性水平α下的统计量分布及表达式,以及对应的拒绝域如表5-1所示。

表5-1　假设检验的统计量及其他参数