5.4.3 双样本t检验
t检验是用t分布理论来推论差异发生的概率,从而比较两个平均数的差异是否显著。一般用于样本数量较小的情况,样本数小于30。
Excel提供的“双样本t-检验”分析工具基于每个样本检验样本总体平均值的等同性。这三个工具分别使用不同的假设:样本总体方差相等;样本总体方差不相等;两个样本代表同一主体处理前后的观察值。
对于这三个工具,t-统计值t在输出表中计算并统一显示为“t Stat”。数据决定了t是负值还是非负值。假设基于相等的基础总体平均值,如果t<0,则“P(T<=t)单尾”返回t-统计的观察值比t更趋向负值的概率。如果t≥0,则“P(T<=t)单尾”返回t-统计的观察值比t更趋向正值的概率。“t单尾临界值”返回截止值,这样,t-统计的观察值将大于或等于“t单尾临界值”的概率就为Alpha。“P(T<=t)双尾”返回t-统计的观测值绝对值大于t的概率。“P双尾临界值”返回截止值,这样t-统计的观测值绝对值大于“P双尾临界值”的概率就为Alpha。
1.t-检验:成对双样本平均值
当样本中存在自然配对的观察值时(例如,对一个样本组在实验前后进行了两次检验),可以使用此成对检验。此分析工具及其公式可以进行成对双样本学生的t-检验,以确定取自处理前后的观察值是否来自具有相同总体平均值的分布。此t-检验窗体并未假设两个总体的方差是相等的。
注意:由此工具生成的结果中包含合并方差,亦即数据相对于平均值的离散值的累积测量值,可以由下面的公式得到:
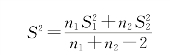
例5.9 应用某药物A治疗患者10名,治疗前后血红蛋白的含量(单位:g%)如表5-7所示,问该药物是否会引起血红蛋白的变化。
表5-7 某药物A治疗前后病人血红蛋白变化表

【t-检验步骤】
按照题意检验假设
H 0:μ1=μ2;H 1:μ1≠μ2
(1)把数据按照“列”的方式排列,如图5-40所示。
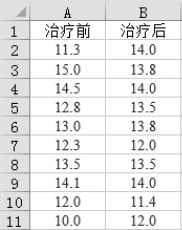
图5-40 按列录入数据
(2)选择“数据”选项卡,然后单击“分析”组的“数据分析”工具中的“t-检验:成对双样本平均值”。
(3)设置“t-检验:平均值的成对二样本分析”参数,如图5-41所示。
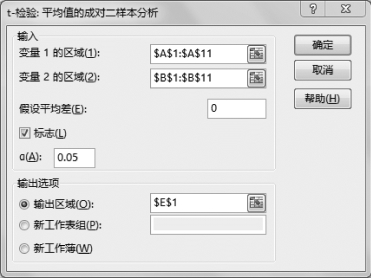
图5-41 “t-检验:平均值的成对二样本分析”参数
•输入变量1的区域:$A$1:$A$11,选中变量1的数据区域。
•输入变量2的区域:$B$1:$B$11,选中变量2的数据区域。
•标志:√,如果变量区域选中了标题行,则单击,否则不单击。
•输出区域:$E$1,可自行单击。
(4)得到“t-检验:成对双样本平均值”分析结果,如图5-42所示。
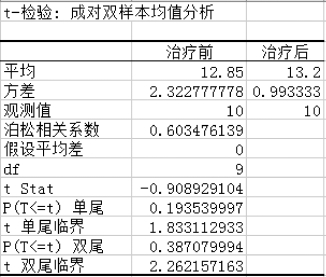
图5-42 “t-检验:成对双样本均值分析”结果
(5)结论:因为P=0.387 1>0.05,所以服用该药物治疗后,未引起血红蛋白显著性变化。
2.t-检验:双样本方差假设
t-检验:双样本方差假设又分为双样本等方差假设与双样本异方差假设。双样本等方差假设分析工具可进行双样本学生t-检验。此t-检验窗体先假设两个数据集取自具有相同方差的分布,故也称作同方差t-检验。可以使用此t-检验来确定两个样本是否可能来自具有相同总体平均值的分布。
双样本异方差假设分析工具可进行双样本学生t-检验。此t-检验窗体先假设两个数据集取自具有不同方差的分布,故也称作异方差t-检验。如同上面的“等方差”情况,可以使用此t-检验来确定两个样本是否可能来自具有相同总体平均值的分布。当两个样本中有截然不同的对象时,可使用此检验。当具有唯一的一组对象以及代表每个对象在处理前后的测量值的两个样本时,则应使用下面所描述的成对检验。
用于确定统计值t的公式如下:
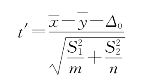
下列公式可用于计算自由度df。因为计算结果一般不是整数,所以df的值被舍入为最接近的整数,以便从t表中获得临界值。因为使用非整数df值有可能计算T.TEST值,所以Excel工作表函数T.TEST使用未进行舍入的df计算值。由于这些决定自由度的不同方式,T.TEST函数和此t-检验工具的结果在“异方差”情况中将不同。
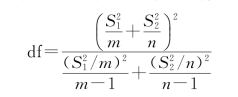
当遇到问题时,首先应利用两个总体方差的F-检验判断该问题是双样本等方差还是异方差,再根据F-检验的结论,进一步进行分析。
例5.10 某医院研究某药物对A疾病的诊断价值,用随机抽样的方法比较了20名A疾病患者与20名健康人某项指标(%)的差别,数据如下:
A疾病患者:145 167 144 136 147 129 129 148 130 123 132 143 132 143 139 150 148 137 133 140
健康人:131 123 141 135 146 130 125 136 136 125 140 133 142 141 134 142 143 148 143 136
问该项指标在两组之间是否存在明显差别。
【实验步骤】
首先进行“F-检验 双样本方差”分析,判断A疾病患者与健康人该项指标数据方差是否相同。
(1)把数据按照“列”的方式排列,如图5-43所示。
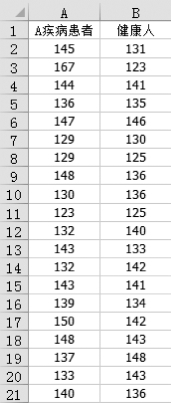
图5-43 按列录入数据
(2)选择“数据”选项卡,然后单击“分析”组的“数据分析”工具中的“F-检验:双样本方差分析”。
(3)设置“F-检验:双样本方差”参数,如图5-44所示。
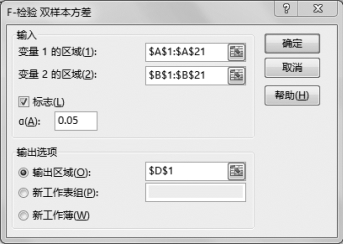
图5-44 “F-检验:双样本方差”参数
•输入变量1的区域:$A$1:$A$21,选中变量1的数据区域。
•输入变量2的区域:$B$1:$B$21,选中变量2的数据区域。
•标志:√,如果变量区域选中了标题行,则单击,否则不单击。
•输出区域:$D$1(可自行单击)。
(4)得到“F-检验:双样本方差分析”结果,如图5-45所示。(https://www.daowen.com)
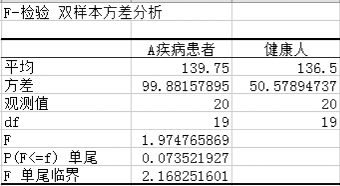
图5-45 “F-检验:双样本方差分析”结果
(5)因为F-统计值小于f的概率为0.07>0.05,且F=1.97小于F单尾临界2.168,均可以判断A疾病患者和健康人的两样本方差无明显差异,可以认为相同。由该结论,我们选择“t-检验:双样本等方差假设”工具。
(6)选择“数据”选项卡,然后单击“分析”组的“数据分析”工具中的“t-检验:双样本等方差假设”。
(7)设置“t-检验:双样本等方差假设”参数,如图5-46所示。
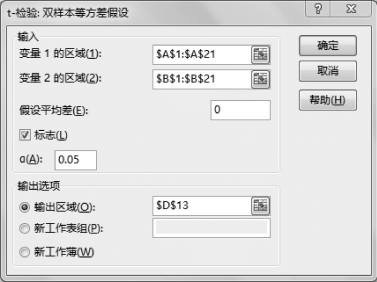
图5-46 “t-检验:双样本等方差假设”参数
•输入变量1的区域:$A$1:$A$21,选中变量1的数据区域。
•输入变量2的区域:$B$1:$B$21,选中变量2的数据区域。
•假设平均差:0。
•标志:√,如果变量区域选中了标题行,则单击,否则不单击。
•输出区域:$D$13,可自行单击。
(8)得到“t-检验:双样本等方差假设”结果,如图5-47所示。
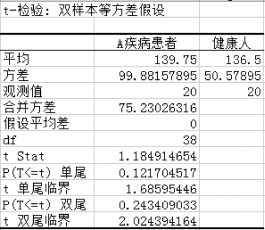
图5-47 “t-检验:双样本等方差假设”结果
【结论】
因为“P(T<=t)双尾”=0.243 4>0.05,所以得到最后结果,该项指标在两组之间不存在显著性差别。
下面我们将数据修改一下,看一下“t-检验:双样本异方差假设”的情况。
例5.11 某医院研究某药物对B疾病的诊断价值,随机抽样的方法比较了20名B疾病患者与20名健康人某项指标(%)的差别,数据如下:
B疾病患者:188 190 161 195 172 177 168 160 168 176 176 173 197 156 160 153 185 185 181 196
健康人:131 123 141 135 146 130 125 136 136 125 140 133 142 141 134 142 143 148 143 136
问该项指标在两组之间是否存在明显差别。
【实验步骤】
首先进行“F-检验 双样本方差”分析,判断A疾病患者与健康人该项指标数据方差是否相同。
(1)把数据按照“列”的方式排列,如图5-48所示。
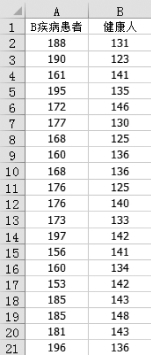
图5-48 按列录入数据
(2)选择“数据”选项卡,然后单击“分析”组的“数据分析”工具中的“F-检验:双样本方差分析”。
(3)设置“F-检验:双样本方差”参数,如图5-49所示。
图5-49 “F-检验:双样本方差”参数
•输入变量1的区域:$A$1:$A$21,选中变量1的数据区域。
•输入变量2的区域:$B$1:$B$21,选中变量2的数据区域。
•标志:√,如果变量区域选中了标题行,则单击,否则不单击。
•输出区域:$D$1(可自行单击)。
(4)得到“F-检验:双样本方差分析”结果,如图5-50所示。
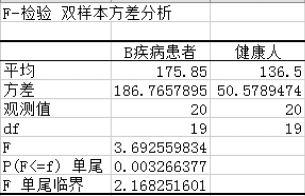
图5-50 “F-检验:双样本方差分析”结果
(5)因为F-统计值小于f的概率为0.003 3<0.05,且F=3.693>2.168,均可以判断B疾病患者和健康人的两样本方差具有明显差异,可以认为不相同。由该结论,我们选择“t-检验:双样本异方差假设”工具。
(6)选择“数据”选项卡,然后单击“分析”组的“数据分析”工具中的“t-检验:双样本异方差假设”。
(7)设置“t-检验:双样本异方差假设”参数,如图5-51所示。
•输入变量1的区域:$A$1:$A$21,选中变量1的数据区域。
•输入变量2的区域:$B$1:$B$21,选中变量2的数据区域。
•假设平均差:0。
•标志:√,如果变量区域选中了标题行,则单击,否则不单击。
•输出区域:$H$1,可自行单击。
图5-51 “t-检验:双样本异方差假设”参数
(8)得到“t-检验:双样本异方差假设”结果,如图5-52所示。
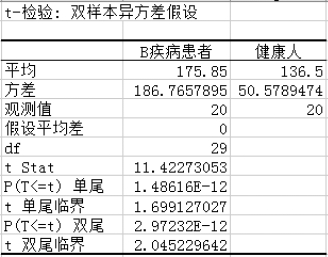
图5-52 “t-检验:双样本异方差假设”结果
【结论】
因为“P(T<=t)双尾”=2.972 32×10-12<0.05,所以得到最后结果,该项指标在两组之间存在显著性差别。
