7.2 回归分析
在客观世界中普遍存在着变量之间的关系。变量之间的关系一般来说可分为确定性的与非确定性的两种。确定性关系是指变量之间的关系可以用函数关系来表达的。另一种非确定性关系即所谓相关关系。例如人的身高与体重之间存在着关系,一般来说,人高一些,体重要重一些,但同样高度的人,体重往往不相同。人的血压与年龄之间也存在着关系,但同年龄的人的血压往往不相同。气象中的温度与湿度之间的关系也是这样。这是因为我们涉及的变量(如体重、血压、湿度)是随机变量,上面所说的变量关系是非确定性的。
回归分析是应用极其广泛的数据分析方法之一。它基于观测数据建立变量间适当的依赖关系,以分析数据内在规律,并可用于预报、控制等问题。回归分析则要分析现象之间相关的具体形式,确定其因果关系,并用数学模型来表现其具体关系。比如说,从相关分析中我们可以得知“质量”和“用户满意度”变量密切相关,但是这两个变量之间到底是哪个变量受哪个变量的影响,影响程度如何,则需要通过回归分析方法来确定。具体分析是对具有相关关系的现象,选择一适当的数学关系式,用以说明一个或一组变量变动时,另一个变量或一组变量平均变动的情况。在回归分析中,把变量分为两类。一类是因变量,它们通常是实际问题中所关心的变量,一般用Y表示;而影响因变量取值的另一类变量称为自变量,自变量通常是实际问题中的条件,一般用X来表示。
模型完整(没有包含不该进入的变量,也没有漏掉应该进入的变量)的误差相互独立且服从标准正态分布。然而,现实数据常常不能完全符合上述假定,因此统计学家研究出许多回归模型来解决线性回归模型假定过程的约束。回归分析研究的一般方法如下。
(1)确定变量
明确预测的具体目标,也就确定了因变量。如果预测具体目标是下一年度的销售量,那么销售量Y就是因变量。通过市场调查和查阅资料,寻找预测目标的相关影响因素,即自变量,并从中选出主要的影响因素。
(2)建立预测模型
依据自变量和因变量的历史统计资料进行计算,在此基础上建立回归分析方程,即回归分析预测模型。
(3)进行相关分析
回归分析是对具有因果关系的影响因素(自变量)和预测对象(因变量)所进行的数理统计分析处理。只有当变量与因变量确实存在某种关系时,建立的回归方程才有意义。因此,作为自变量的因素与作为因变量的预测对象是否有关,相关程度如何,以及判断这种相关程度的把握性多大,就成为进行回归分析必须要解决的问题。进行相关分析,一般要求出相关关系,以相关系数的大小来判断自变量和因变量的相关程度。
(4)计算预测误差
回归预测模型是否可用于实际预测,取决于对回归预测模型的检验和对预测误差的计算。回归方程只有通过各种检验,且预测误差较小,才能将回归方程作为预测模型进行预测。(https://www.daowen.com)
(5)变量的显著性检验
回归分析是要判断解释变量X是否是被解释变量Y的一个显著性的影响因素。在一元线性模型中,就是要判断X是否对Y具有显著的线性影响,这就需要进行变量的显著性检验。一个变量是显著的,也就是在回归方程中的系数不为0,由此,可以提出原假设与备择假设:
![]()
构造t统计量,并由样本计算其值
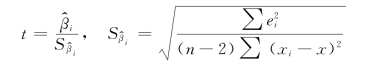
根据给定显著性水平,判断统计量的值是否落在拒绝域内。
(6)确定预测值
利用回归预测模型计算预测值,并对预测值进行综合分析,确定最后的预测值。根据实测数据来求解模型的各个参数。
(7)评价回归模型
评价回归模型是否能够很好地拟合实测数据,如果能够很好地拟合,则可以根据自变量进一步预测。
回归方程是根据样本资料通过回归分析所得到的反映因变量和自变量回归关系的数学表达式。一般在实际应用中,线性回归方程应用得比较多。根据不同的回归分析方法得到不同的回归方程,这些都是合理的,我们可以通过分析标准误差和拟合优度,选择合适的回归方程。Excel 2019提供了散点图和回归工具两种方法进行回归分析。
