6.1 单因素实验
单因素分析,顾名思义,就是在实验过程中只有一个因素,或者处理为只有一个因素发生作用。例如,研究肥料对作物产量的影响、生长素对植物苗高的影响等,实验中的肥料因素和生长素因素均为单一的实验处理。
Excel提供的单因素分析工具对两个或两个以上样本的数据方差执行简单的分析。此分析可提供一种假设检验,该假设的内容是:每个样本都取自相同基础概率分布,这与对所有样本来说基础概率分布都不相同的假设相反。如果只有两个样本,可以使用工作表函数T.TEST。对于两个以上的样本,并无T.TEST的适宜推广形式,此时可调用单因素方差分析模型。
单因素实验的方差分析:设因素A有s个水平A 1,A 2,…,As,在水平A j(j=1,2,…,s)下,进行n j(n j≥2)次独立实验,得到如表6-1所示的结果。
表6-1 单因素方差分析
我们假定:各个水平A j(j=1,2,…,s)下的样本X 1j,X 2j,…,X njj来自具有相同方差σ2、均值分别为μj(j=1,2,…,s)的正态总体N(μj,σ2),μj与σ2未知。且设不同水平A j下的样本之间相互独立。
由于N ij～N(μj,σ2),即有Xij-μj～N(0,σ2),故Xij-μj可看成是随机误差。记Xij-μj=εij,则X ij可写成
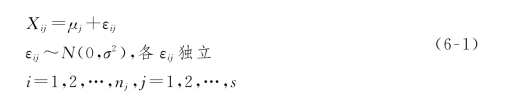
其中,μj与σ2均为未知参数。式(6-1)称为单因素实验方差分析的数学模型。这是本节的研究对象。
方差分析的任务是对于式(6-1):
①检验s个总体N(μ1,σ2),…,N(μs,σ2)的均值是否相等,即检验假设
②作出未知参数μ1,μ2,…,μs,σ2的估计。式(6-2)的拒绝域为
表6-2所示为单因素实验方差分析表。
表6-2 单因素实验方差分析表
表中
=SA/(s-1)
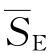=S E/(n-s)分别称为SA、S E的均方。另外,因在S T中n个变量X ij-
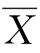之间仅满足一个约束条件,故S T的自由度为n-1。
在实际中,我们可以按以下较简便的公式来计算S T、SA和S E。
记
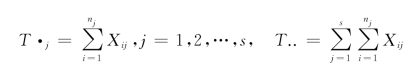
即有
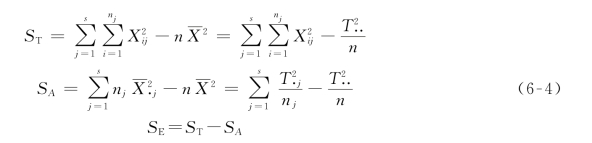
Excel数据分析的“方差分析:单因素方差分析”为我们提供了简单方便的操作,下面通过例题说明。
例6.1 设有三台机器,用来生产规格相同的铝合金薄板。取样,测量薄板的厚度,精确至1/1 000 cm。测量结果如表6-3所示。
表6-3 铝合金板的厚度
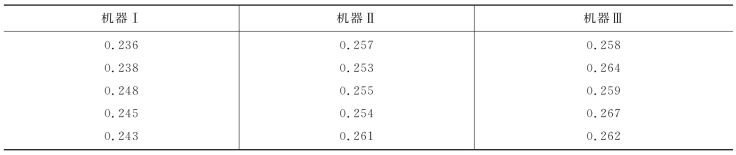
这里实验的指标是薄板的厚度,机器为因素,不同的三台机器就是这个因素的三个不同的水平。我们假设除机器这一因素外,材料的规格、操作人员的水平等其他条件都相同,这就是单因素实验。实验的目的是为了考察各台机器所生产的薄板的厚度有无显著性差异,即为了考察机器这一因素对厚度有无显著性的影响。如果厚度有显著性差异,就表明机器这一因素对厚度的影响是显著的。
【单因素方差分析步骤】
(1)将实验数据录入Excel表中,注意按照机器类型按列(或行)录入,如图6-1所示。
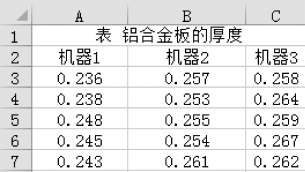
图6-1 按列录入数据
(2)选择“数据”选项卡,然后单击“分析”组的“数据分析”工具中的“方差分析:单因素方差分析”。
(3)设置“方差分析:单因素方差分析”参数,如图6-2所示。
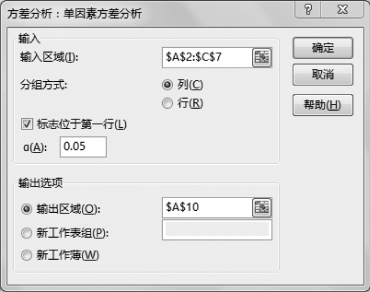
图6-2 “方差分析:单因素方差分析”参数
•输入区域:$A$2:$C$7,这里单击实际数据区域。
•分组方式:列。按行录入数据,单击“行”;按列录入数据,单击“列”。
•标志位于第一行:√。如果输入区域中未单击标题行,则不单击。
•α:0.05。根据实验要求的显著性水平填写。
•输出区域:$A$10。这里可自行单击。
(4)单因素方差分析结果如图6-3所示。
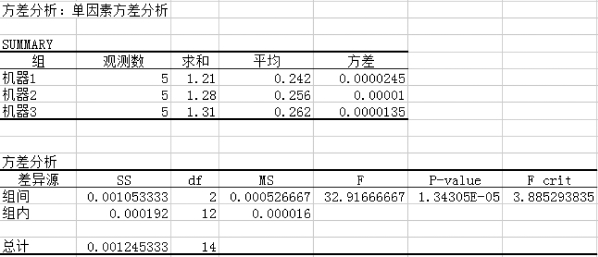
图6-3 “方差分析:单因素方差分析”结果
“方差分析:单因素方差分析”结果解释:
•在SUMMARY(摘要)中,计算出三个机器的观测数、和、平均值与方差。
•方差分析:
✧SS表示离均差平方和,也就是变量中每个数据点与变量均值差的平方和;
✧df表示自由度;
✧MS表示均方,MS的值等于对应的SS除以df;
✧F表示F统计量,是方差分析中用于假设检验的统计量,其值等于处理的MS除以误差的MS;
✧P-value表示概率值;
✧F crit表示在0.05的显著性水平下F的临界值。
【结论】
F=32.92＞F cirt=3.885,F值落入拒绝域,因此三个机器生产的薄板厚度差异显著。
除了观察F值以外,我们还可以观察P-value的值,因为P-value=1.343 05×10-5＜0.05,所以落入拒绝域,因此可以得到同样的结论,三个机器生产的薄板厚度差异显著。
在Excel结论区域可以录入“=IF(F21＜0.05,"三个机器生产的薄板厚度差异显著","三个机器生产的薄板厚度差异不显著")”,迅速判断出结果:机器这一因素对厚度的影响是显著的。