2.5 综合实验
【实验2.1】 正态分布函数实验
有甲、乙、丙3家投资公司对某投资组合的收益标准差预计相同,都认为是0.05。但是这3家投资公司对于投资组合的平均收益估计不同,分别认为是0.1、0.2和0.3。根据这些信息,绘制出3家投资公司对投资组合期望收益的分布情况。
【实验步骤】
(1)在单元格A2中输入“-0.1”。
(2)选中单元格A2,选择“开始”选项卡“编辑”组“填充”下列菜单中的“序列”命令,在“序列”命令对话框中填写合适的参数,如图2-9所示。
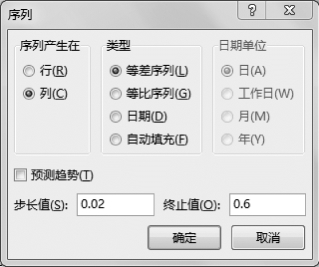
图2-9 生成等差序列
(3)选中单元格B2,输入“=NORM.DIST(A2,$B$1,0.05,0)”。
NORM.DIST函数解析:
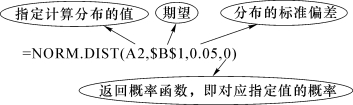
将公式复制到区域B3:B37,如图2-10所示。
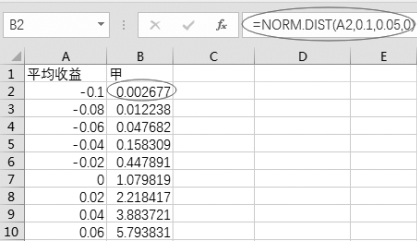
图2-10 求均值为0.1的正态分布函数值
(4)选中单元格C2,输入“=NORM.DIST(A2,0.2,0.05,0)”,将公式复制到区域C3:C37。
(5)选中单元格D2,输入“=NORM.DIST(A2,0.3,0.05,0)”,将公式复制到区域D3:D37,结果如图2-11所示。
(6)选中区域B1:D37,依次选择“插入”→“图表”→“折线图”→“二维折线图”→“带数据标记的折线图”命令,如图2-12所示。
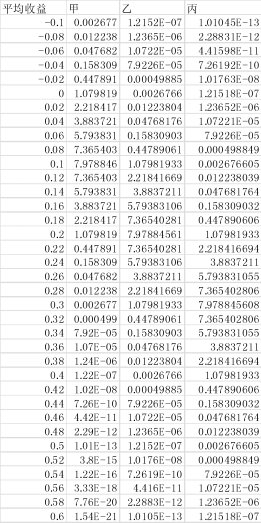
图2-11 甲、乙、丙三家公司投资组合期望收益正态分布函数值
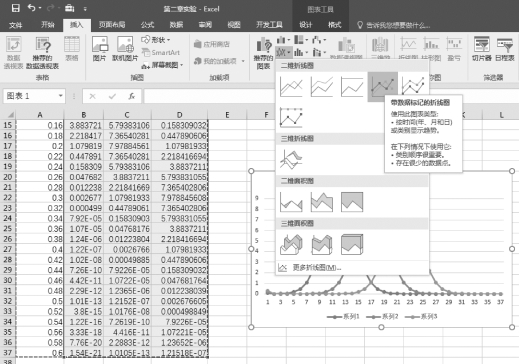
图2-12 生成二维折线图
生成初始图表如图2-13所示。
(7)选中初始图表,选择“图表”工具“设计”选项卡“数据”组的“选择数据”命令,在“选择数据源”对话框中单击“水平(分类)轴标签”下方的“编辑”按钮,如图2-14所示。
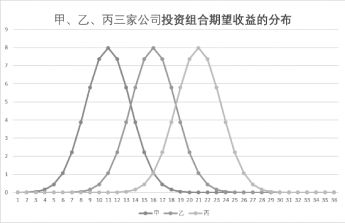
图2-13 初始图表
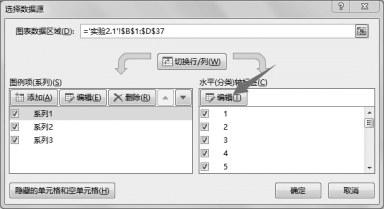
图2-14 选择数据源
在“编辑”对话框中,选择A1:A37区域,如图2-15所示。
图2-15 选择轴标签
整理后得到甲、乙、丙三家公司投资组合期望收益分布图,如图2-16所示。(https://www.daowen.com)
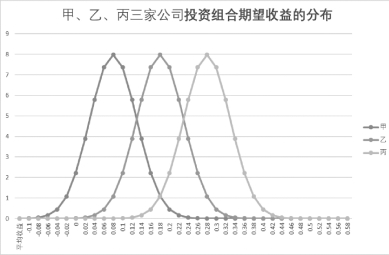
图2-16 甲、乙、丙三家公司投资组合期望收益分布图
【实验2.2】 抽样分布常见函数实验
已知某公司2014—2017年第一季度的两个数据,如图2-17所示。
(1)统计每年一月份的“数据二”的和;
(2)统计“数据一”和“数据二”区域数字的个数;
(3)统计“数据一”中以字母A开始的数据的个数;
(4)统计“数据一”中值小于20的数据的个数;
(5)统计四年来二月份的“数据二”的平均值;
(6)统计“数据二”中大于等于10小于等于25的数据个数。
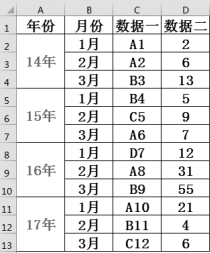
图2-17 某公司第一季度数据表
【实验步骤】
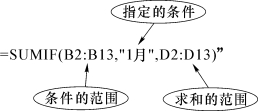
(1)在指定单元格中输入“=SUMIF(B2:B13,"1月",D2:D13)”,结果为40。
SUMIF函数解析:
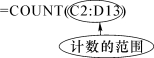
(2)在指定单元格中输入“=COUNT(C2:D13)”,结果为12。
COUNT函数解析:
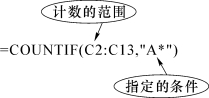
(3)在指定单元格中输入“=COUNTIF(C2:C13,"A*")”,结果为5。
COUNTIF函数解析:
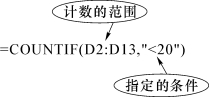
(4)在指定单元格中输入“=COUNTIF(D2:D13,"<20")”,结果为9。
COUNTIF函数解析:
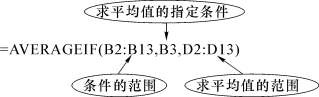
(5)在指定单元格中输入“=AVERAGEIF(B2:B13,B3,D2:D13)”,结果为12.5。
AVERAGEIF函数解析:
(6)在指定单元格中输入“=COUNTIF(D2:D13,"<=25")-COUNTIF(D2:D13,"<10")”,结果为3。
COUNTIF(D2:D13,"<=25")表示在D2:D13单元格区域内小于等于25的数字的个数,结果为10;COUNTIF(D2:D13,"<10")表示在D2:D13单元格区域内小于10的数字的个数,结果为7;它们的差即为大于等于10小于等于25的数字的个数。
