8.4 指数平滑法
指数平滑法是在移动平均法的基础上发展起来的一种时间序列分析预测法,它通过计算指数平滑值,配合一定的时间序列预测模型对现象的未来进行预测。其原理是任一期的指数平滑值都是本期实际观察值与前一期指数平滑值的加权平均,相当于用本期的实际值对预测值进行不断的修正,以适应数据的变化。一次指数平滑法是一种加权预测,权数为α。它既不需要存储全部历史数据,也不需要存储一组数据,从而可以大大减少数据存储问题,甚至有时只需一个最新观察值、最新预测值和α值,就可以进行预测。它提供的预测值是前一期预测值加上前期预测值中产生的误差的修正值。
式中
表示t+1期的预测值;Y t表示t期的真实值;
表示t期的预测值;α表示平滑系数,α∈[0,1];1-α表示阻尼系数。
由该公式可知:
①
是Y t和
的加权算数平均数,随着α取值的大小变化,决定Y t和
对
的影响程度,当α=1时
=Y t;当α=0时
。
②
具有逐期追溯性质,可探源至
为止,包括全部数据。其过程中,平滑常数以指数形式递减,故称为指数平滑法。平滑常数决定了平滑水平以及对预测值与实际结果之间差异的响应速度。平滑常数α越接近于1,远期实际值对本期平滑值影响程度的下降越迅速;平滑常数α越接近于0,远期实际值对本期平滑值影响程度的下降越缓慢。由此,当时间数列相对平稳时,可取较大的α;当时间数列波动较大时,应取较小的α,以不忽略远期实际值的影响。
指数平滑法的工作流程如图8-10所示。
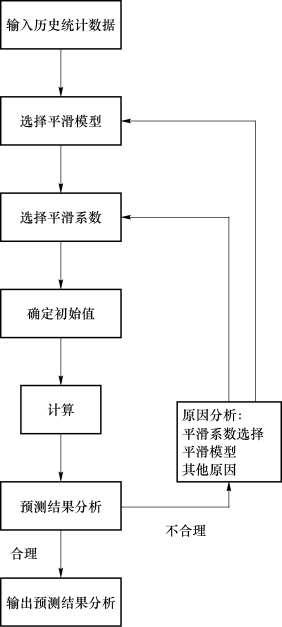
图8-10 指数平滑法工作流程图
例8.4 某公司2006—2018年投资总额(单位:万元)数据如表8-7所示。
表8-7 某公司2006—2018年投资总额表
已知该公司的阻尼系数为0.2,计算2007—2018年的预测值,并进一步预测该公司2019年的投资总额。
【实验步骤】
(1)按列录入表数据,预设1-α=0.2,那么α的值就是0.8,因此在单元格D1中输入“=1-B1”,如图8-11所示。
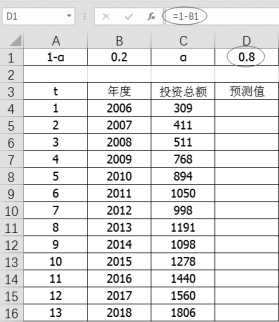
图8-11 预设阻尼系数与平滑系数
(2)选择“数据”选项卡“分析”组中的“数据分析”选项,单击“指数平滑”命令,如图8-12所示。
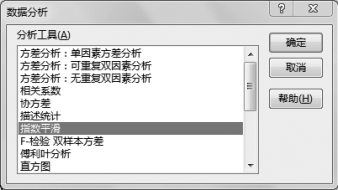
图8-12 单击指数平滑命令
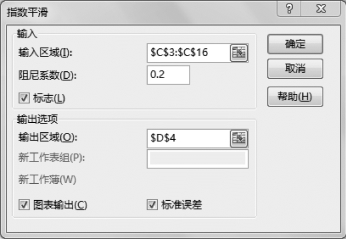
(3)设置指数平滑参数,如图8-13所示。
图8-13 设置指数平滑参数
•输入区域:$C$3:$C$16,即数据的所在区域;
•阻尼系数:0.2,根据实际数字填写。
•标志:√。如果输入区域包括标题行,则勾选“标志”复选框;如果输入区域不包括标题行,则保持“标志”前的复选框空白。
•输出区域:$D$4,输出区域可以任意单击。
•图表输出:√;
•标准误差:√。
【实验结果】
2006—2018年的预测值及误差如图8-14所示。
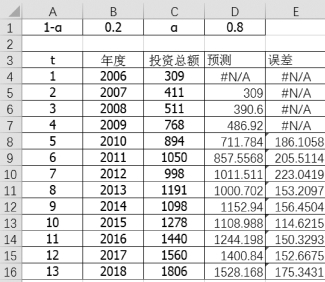
图8-14 指数平滑法预测值及误差
指数平滑实际值与预测值如图8-15所示。
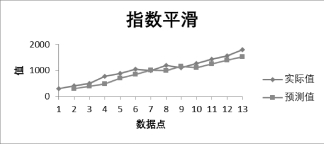
图8-15 指数平滑图
【结论】
由上述分析可知,2018年实际值为1 806,预测值为1 528.168,因此2019年预测值为
本例中可在指定单元格中输入“=C16*D1+D16*B1”。
本例中,阻尼系数为0.2,如果阻尼系数更改为0.15,那么可以得到一个新的预测值1765.767,如图8-16所示。
不同的阻尼系数会导致不同的结果,那么是否存在一个最佳阻尼系数,帮助我们找到最优化的预测结果呢?下面我们将介绍最佳阻尼系数的求解。
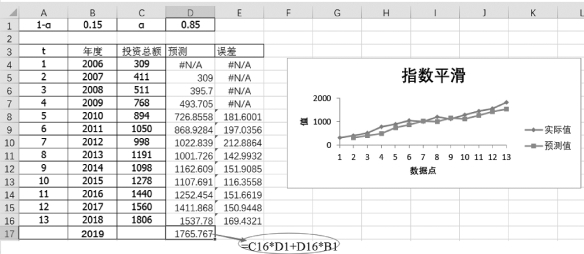
图8-16 阻尼系数为0.15条件下的指数平滑结果