9.2 判别分析
判别分析又称“分辨法”,是在分类确定的条件下,根据某一研究对象的各种特征值判别其类型归属问题的一种多变量统计分析方法。其基本原理是按照一定的判别准则,建立一个或多个判别函数,用研究对象的大量资料确定判别函数中的待定系数,并计算判别指标,据此即可确定某一样本属于何类。得到一个新的样品数据,要确定该样品属于已知类型中哪一类,这类问题属于判别分析问题。例如,某些昆虫的性别只有通过解剖才能够判别,但雄性和雌性昆虫在若干体表度量上有些综合的差异。人们就根据已知的雌雄昆虫体表度量得到一个标准,并以此标准来判别其他未知性别的昆虫。这样虽非100%准确的判别,但至少大部分是对的,而且用不着杀生。这个过程就是判别分析。
那么本节的判别分析和9.1节的聚类分析有何不同呢?在聚类分析中,人们一般事先并不知道应该分成几类,更别说哪几类了,聚类分析中的分类问题全根据数据确定。但判别分析是在已知对象有若干类型和一批已知样品的观测数据的基础上根据某些准则建立判别式。在判别分析中,至少有一个已经明确知道类别的“训练样本”,利用该样本来建立判别准则,并通过预测变量来为未知类别的观测值进行判别。因此,判别分析中的变量或指标必须确实与分类有关,个体的观测值必须准确,个体的数目必须足够多,实际实验的时候,可以先通过聚类分析以得知分类,然后再根据分类进行判别。
银行为了对贷款进行管理,需要预测哪些类型的客户可能不会按时归还贷款。已知过去几年中700个客户的贷款归还信誉度,据此可以将客户分成两组:可靠客户和不可靠客户。再通过收集客户的一些资料,如年龄、工资收入、教育程度、存款等,将这些资料作为自变量。通过判别分析建立判别函数。那么,如果有新客户提交贷款请求,就可以利用已经创建好的判别函数,对新客户进行判别分析。
判断分析的基本步骤:
(1)根据研究目的确定研究对象或者研究样本及其所用的指标;
(2)收集数据,得到训练样本;
(3)用判别分析方法得到判别函数;
(4)对该判别函数是否有实用价值进行考核;
(5)实际应用。
判别函数
Y=a 1 x 1+a 2 x 2+…+a nx n
其中:Y为判别分数,即判别值;x i为反映研究对象特征的变量;ai为系数。
对于分为m类的研究对象,建立m个判别函数。
关于判别分析的假定:
(1)预测对象服从正态分布;
(2)预测对象没有显著的相关性;
(3)预测对象的平均值和方差不相关;
(4)预测对象应是连续变量,因变量是间断变量;
(5)两个预测对象之间的相关性在不同类中是一样的。
判别分析的各阶段必须注意,事前组别类的分类标准(作为判别分析的因变量)要尽可能准确和可靠,否则会影响判别函数的准确性,从而影响判别分析的效果。所分析的自变量应是因变量的重要影响因素,应该挑选既有重要特征又有区别能力的变量,达到以最少变量获得最高辨别能力的目标。
下面介绍判别分析常用的距离判别法。
距离判别法的基本思想:首先根据已知分类的数据分别计算各类的重心(均值),对任给的一次观测,若它与第i类的重心距离最近,则判断它来自第i类。
在距离判别法中,主要使用马氏距离。马氏距离是由印度统计学家马哈拉诺比斯提出的,表示数据的协方差距离。
d=(x-μ)'Σ-1 (x-μ)
马氏距离是一种有效的计算两个未知样本集的相似度的方法,与欧氏距离不同的是马氏距离考虑到各种特性之间的联系。例如,一条关于身高的信息会带来一条关于体重的信息,因为身高和体重是有关联的,这种关联与尺度无关,独立于测量尺度。如果协方差矩阵为单位矩阵,那么马氏距离就简化为欧氏距离,如果协方差矩阵为对角阵,则其也可称为正规化的欧氏距离。
设有两个p维类别(总体)π1、π2的均值分别为μ1、μ2,协方差分别为Σ1＞0、Σ2＞0。设x是一个待判的p维样品,下面根据两种情况判断x属于哪一类别的样品。
1.第一种情况,当Σ1=Σ2=Σ时的判别
方法1:先计算x与两类别的距离d( x,π1)和d( x,π2),然后根据以下规定进行判别:
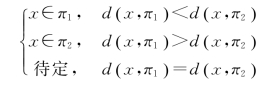
这个判别规则称为最小距离判别,即x与哪个类别的距离小,那么x就属于哪一类。当d( x,π1)=d( x,π2)时,无法判断x属于哪一类。
方法2:令
,其中
,然后根据以下规定进行判别:
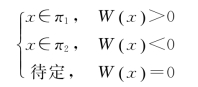
方法2实际上是方法1的变形,这里就不加以证明了。
当μ1、μ2、Σ未知时,可通过样本来估计:
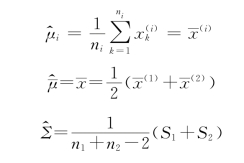
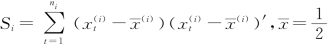
其中,
表示πi的样本
表示πi的样本均值,
2.第二种情况,当Σ1≠Σ2时的判别
方法1:先计算d( x,π1)=
(x-μ2)]1/2,然后根据以下规定进行判别:
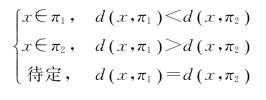
方法2:若令
那么按照以下规则进行判别:
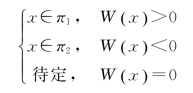
因此,我们在进行判别分析之前,必须进行协方差矩阵是否相等的假设检验。
设x 1,x 2,…,x n是来自多元正态总体N p(μ,Σ),n＞p,Σ＞0的一个样本,μ和Σ未知,要检验的假设是
取-2lnΛ*为检验统计量,在H 0为真时,极限分布为χ2( p( p+1)/2)-分布;对于给定的显著性水平α,如果
则拒绝原假设H 0,否则接受原假设。
这里
例9.4 假设已知某种动物有肉食和素食两种,现有这两种动物的10个样本体内两种物质含量的指标数据,以及它们所属的类别,如图9-51所示。要求根据两种物质的含量对B1、B2和B3三个未知样本进行类别分析。
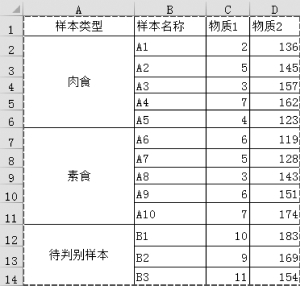
图9-51 样本两种物质含量的指标数据表
在例9.4中已知肉食动物样本A1～A5,素食动物样本A6～A10,待判别样本B1～B3。
【实验步骤】
1.判断肉食动物与素食动物协方差是否相等
H 0:Σ1=Σ2,H 1:Σ1≠Σ2
(1)求解平均值矩阵,即求
平均值矩阵就是分别计算肉食动物和素食动物关于物质1和物质2的数据平均值,如图9-52所示。
•肉食动物物质1的平均值为“=AVERAGE(C2:C6)”;
•肉食动物物质2的平均值为“=AVERAGE(D2:D6)”;
•素食动物物质1的平均值为“=AVERAGE(C7:C11)”;
•素食动物物质2的平均值为“=AVERAGE(D7:D11)”。
图9-52 指标平均矩阵
(2)计算样本协方差矩阵。
①计算肉食动物协方差S 1:
如图9-53所示,
•肉食动物物质1与物质1的协方差为“=COVARIANCE.P(C2:C6,C2:C6)”;
•肉食动物物质1与物质2的协方差为“=COVARIANCE.P(C2:C6,D2:D6)”;
•肉食物质2与物质2的协方差为“=COVARIANCE.P(D2:D6,D2:D6)”。
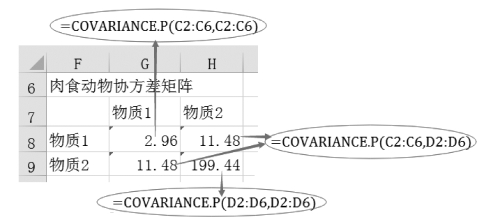
图9-53 肉食动物协方差矩阵
注意:这里计算协方差使用COVARIANCE.P函数。COVARIANCE.P函数返回总体协方差,即两个数据集中每对数据点的偏差乘积的平均数,利用协方差可以确定两个数据集之间的关系。
COVARIANCE.P函数语法:
COVARIANCE.P(ar ray1,ar ray2)
COVARIANCE.P函数语法具有下列参数:
•array1:必需,整数的第一个单元格区域。
•array2:必需,整数的第二个单元格区域。
在Excel 2007中,是用COVAR函数,现在此函数已被替换为COVARIANCE.P函数与COVARIANCE.S函数,这些新函数可提供更高的精确度。
②计算素食动物协方差S 2:
如图9-54所示,
•素食动物物质1与物质1的协方差为“=COVARIANCE.P(C7:C11,C7:C11)”;
•素食动物物质1与物质2的协方差为“=COVARIANCE.P(C7:C11,D7:D11)”;
•素食物质2与物质2的协方差为“=COVARIANCE.P(D7:D11,D7:D11)”。
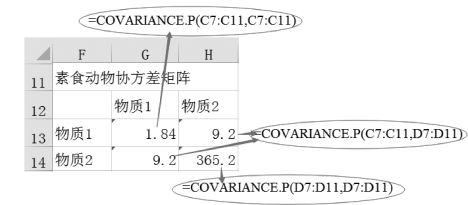
图9-54 素食动物协方差矩阵
(3)计算协方差行列式的值及其对应的对数值:
•计算肉食动物协方差行列式的值为“=MDETERM(G3:H4)”,及其对应的对数值“=LN(F12)”。
•计算素食动物协方差行列式的值为“=MDETERM(G8:H9)”,及其对应的对数值“=LN(F14)”,如图9-55所示。
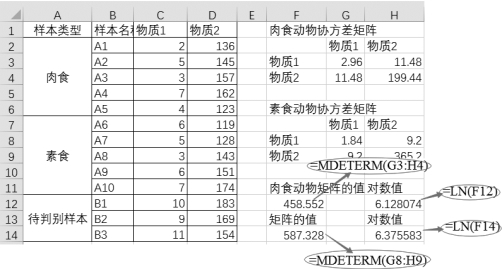
图9-55 计算矩阵的值及其对数值
(4)计算肉食动物协方差的逆矩阵。
①选中K3:L4区域,如图9-56所示。
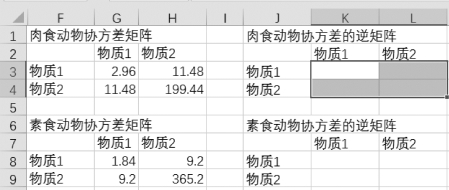
图9-56 选中求逆矩阵区域
②在反白单元格K3中输入“=MINVERSE(G3:H4)”,如图9-57所示。
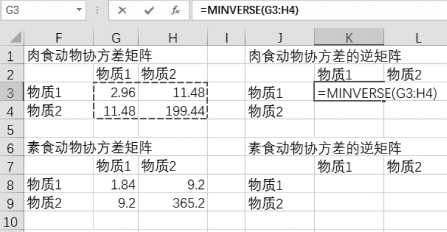
图9-57 MINVERSE函数
注意:这里不能直接按“Enter”键,必须按组合键“Ctrl+Shift+Enter”,结果如图9-58所示。
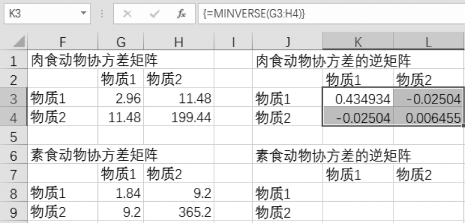
图9-58 按组合键显示结果
(5)计算素食动物协方差的逆矩阵。
选中K8:L9区域,在反白单元格K8中输入“=MINVERSE(G8:H9)”,按组合键“Ctrl+Shift+Enter”,结果如图9-59所示。
(6)计算肉食动物协方差与素食动物协方差逆矩阵的乘积,即
。
选中J12:K13区域,在反白单元格J12中输入=“MMULT(K3:L4,G8:H9)”,按组合键“Ctrl+Shift+Enter”,结果如图9-60所示。
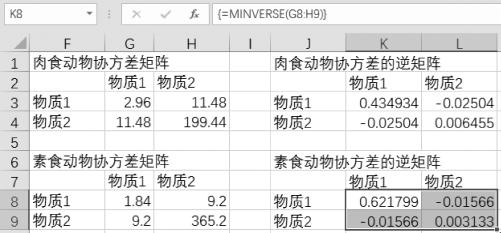
图9-59 计算素食动物协方差逆矩阵
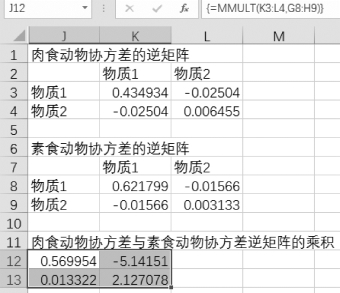
图9-60 求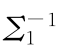
·Σ2
矩阵的迹为“=J12+K13”,结果为2.697 0,如图9-61所示。
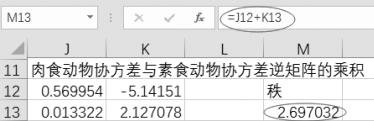
图9-61 求矩阵的迹
(7)计算判断函数“=(5-1)*(H12-H14-2+M13)”,结果为1.798。
函数解析:
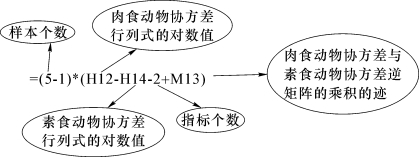
(8)计算
的值“=CHISQ.INV(0.95,2*(2+1)/2)”,结果为7.815,如图9-62所示。
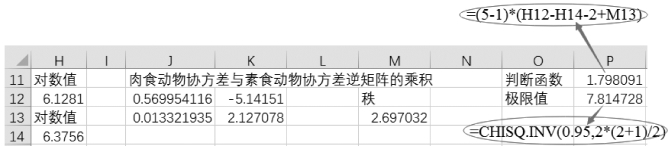
图9-62 计算边界值
【结论】
因为判断函数的值1.798＜7.815,所以不能拒绝H 0,即认为肉食动物的协方差矩阵和素食动物的协方差矩阵相等,如图9-63所示。
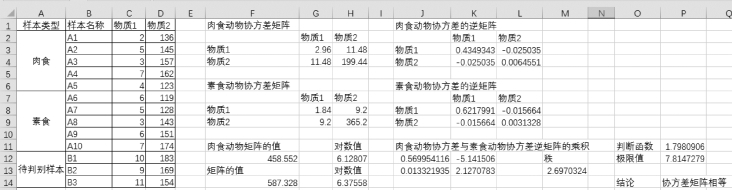
图9-63 判断Σ1=Σ2的工作表
2.在Σ1=Σ2=Σ的条件下进行判断分析
新建一张工作表,将题设数据复制到新表中。
(1)估计总体协方差矩阵Σ^,如图9-64所示。
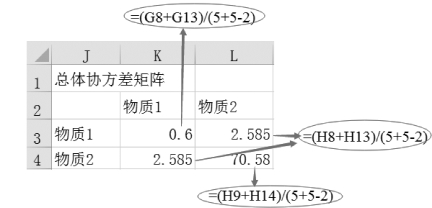
图9-64 估计总体协方差
(2)求解总体协方差矩阵的逆矩阵
①首先选中K8:L9区域,如图9-65所示。
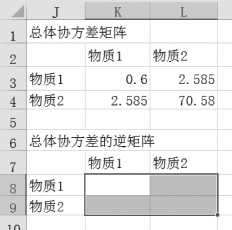
图9-65 选中求逆矩阵区域
②在反白的当前单元格K8中输入“=MINVERSE(K3:L4)”,如图9-66所示。
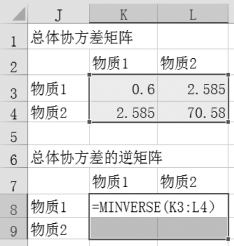
图9-66 输入逆矩阵函数公式
注意:这里不能直接按“Enter”键,必须按组合键“Ctrl+Shift+Enter”,结果如图9-67所示。
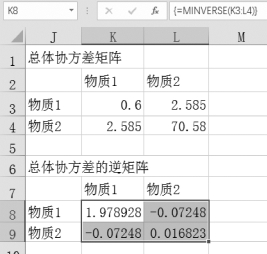
图9-67 求解逆矩阵
(3)计算
,如图9-68所示。
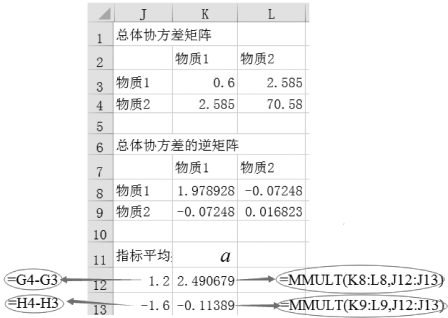
图9-68 计算系数a的值
(4)计算待判样本矩阵—样本均值矩阵
如图9-69所示。
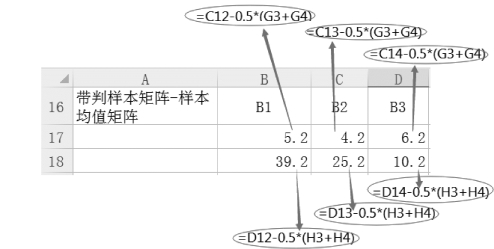
图9-69 计算样本均值矩阵
(5)判别函数
,如图9-70所示。
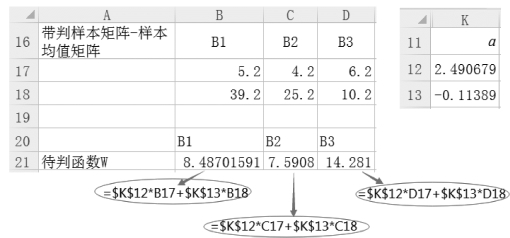
图9-70 求判别函数
【结论】判别函数的值均为正值,所以B1、B2和B3都属于肉食动物。
图9-71所示为判断属于素食或者肉食动物的工作表。
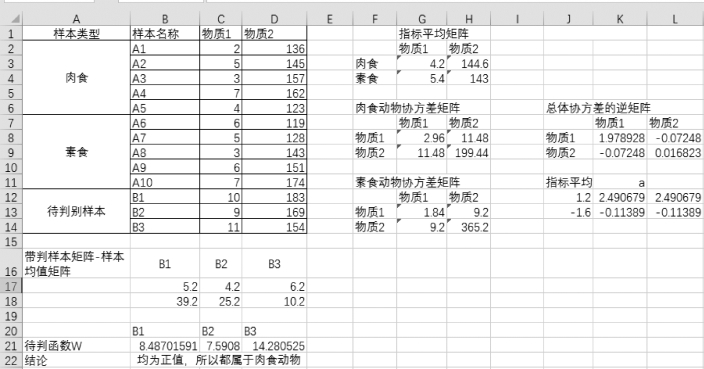
图9-71 判断属于素食或者肉食动物的工作表