5.2.1 方差已知条件下单个正态总体均值的假设检验
根据表5-1的结论可知,在方差已知的条件下,总体服从均值为μ、方差已知为σ2的正态分布。
1.方差已知条件下单侧单个正态总体均值的假设检验
例5.1 公司从生产商处购买牛奶,公司怀疑生产商在牛奶中掺水以牟利。通过测定牛奶的冰点,可以检验出牛奶是否掺水。天然牛奶的冰点温度近似服从正态分布,均值μ0=-0.545℃,标准差σ=0.008℃。牛奶掺水可使冰点温度升高而接近于水的冰点温度0℃。测得生产商提交的5批牛奶的冰点温度,均值为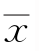
=-0.535℃,问是否可以认为在α=0.05的显著性水平下生产商往牛奶中掺水了呢?
【实验步骤】
按照题意检验假设H 0:μ≤μ0=-0.545(即设牛奶未掺水);H 1:μ＞μ0(即设牛奶已掺水),这是一个右侧检验问题。
【临界值法步骤】
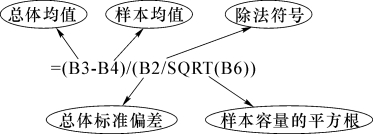
(1)单击单元格B7,计算验证统计量的观测值“=(B3-B4)/(B2/SQRT(B6))”,结果为2.795 084 972。
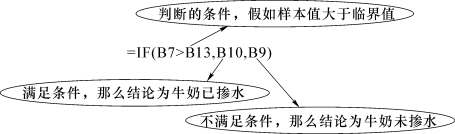
(2)单击单元格B13,计算临界值zα/2“=NORM.S.INV(B5)”,临界值结果为-1.644 853 627。
(3)单击单元格B14,结论为“=IF(B7＞B13,B10,B9)”。
本题中样本值明显大于临界值,因此结论为牛奶已掺水,如图5-2所示。
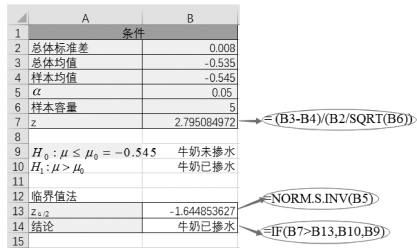
图5-2 方差已知条件下的临界值法
【P值法步骤】
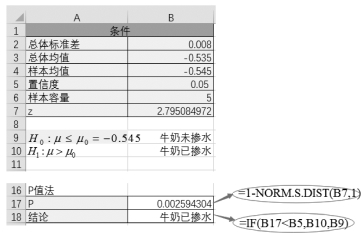
(1)单击单元格B17,计算概率为P值为“=1-NORM.S.DIST(B7,1)”。
这里很多读者可能有一个疑问,为什么统计量对应的概率值P=1-NORM.S.DIST(B7,1)而不直接是直接等于NORM.S.DIST(B7,1)呢?这是因为本题中的概率P表示P{z≥z样本},而Excel函数NORM.S.DIST(B7,1)=Φ(z样本)=P{z＜z样本},表示小于样本值的概率。
(2)单击单元格B18,结论为“=IF(B17＜B5,B10,B9)”,如图5-3所示。
【结论】无论是使用临界值法还是P值法进行实验,两种方法的结论均相同,都是认为该样本牛奶已掺水。
图5-3 方差已知条件下的P值法
2.方差已知条件下双侧单个正态总体均值的假设检验
例5.2 已知某商品的质量服从正态分布,标准差为8。现从中随机抽取20个,如表5-2所示,分析能否在0.05的显著性水平下判断全体的平均值为113。
表5-2 某商品20件样品的质量(单位:kg)
【实验过程】
这是一个双侧检测问题,按照题意检验假设
H 0:μ=μ0=113;H 1:μ≠μ0
【P值法步骤】
(1)单击单元格B11,计算P值为“=MIN(Z.TEST(A2:J3,H5,K5),1-Z.TEST(A2:J3,H5),K5)”。
其中Z.TEST(A2:J3,H5)省略了第3个参数,即用样本标准偏差代替总体标准偏差。
MIN(Z.TEST(A2:J3,H5),1-Z.TEST(A2:J3,H5))表示z检验的左尾概率值与右尾概率值的最小值,结果为0.185 3,如图5-4所示。
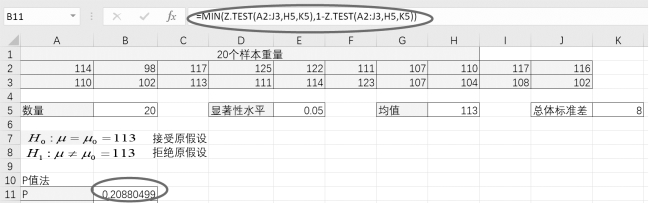
图5-4 计算概率值
(2)单击单元格B12,得到假设检验的结论“=IF(B11＜E5/2,C8,C7)”,如图5-5所示。
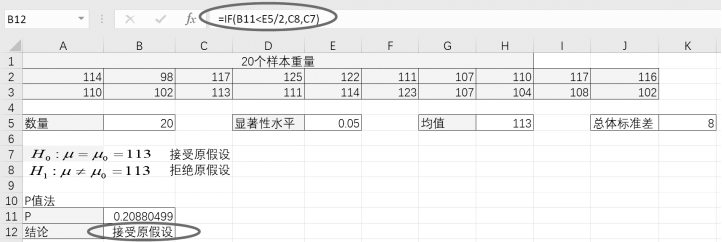
图5-5 P值法的结论
【结论】P值法中的P值为0.185 3＞0.05,因此不拒绝原假设,接受在0.05的显著性水平下全体的平均值为113。