7.3 综合实验
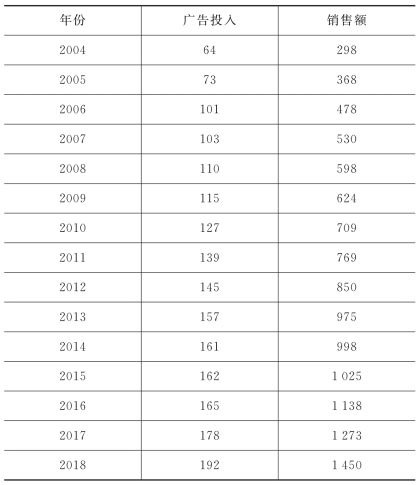
【实验7.1】 表7-7是15年来某公司固定投资与销售收入的数据(单位:万元)资料,今以X表示该公司的广告投入,Y表示相应的销售额,求Y关于X的回归方程。
表7-7 某公司固定投资与销售收入数据
【方法1:散点图法构建线性回归方程】
(1)将数据录入Excel表中,如图7-33所示。
图7-33 按列录入数据
(2)选择“插入”选项卡,然后单击“图表”组的“散点图”选项。
(3)选择“图表工具”中的“设计”选项卡,然后单击“数据”组的“单击数据”选项,并单击数据范围:$B$1:$C$16,如图7-34所示。生成销售额散点图,如图7-35所示。
(4)单击“图表工具”中的“设计”选项卡,然后单击“图表布局”组的“添加图表元素”选项,单击“趋势线”中的“其他趋势线选项”。
图7-34 单击数据
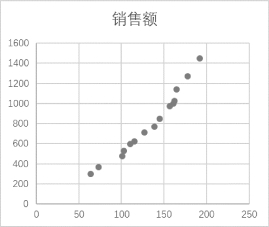
图7-35 销售额散点图
(5)在设置趋势线格式中,选择“线性”;趋势线名称设置为“散点图分析法”;选中“显示公式”和“显示R平方值”复选框,如图7-36所示。
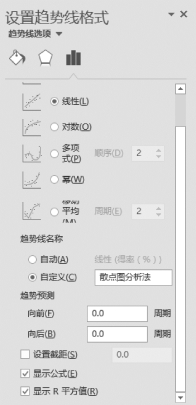
图7-36 设置趋势线格式
(6)在散点图中,出现线性趋势线和线性回归方程:
y=8.687x-348.1
其中R 2=0.959 7,如图7-37所示。
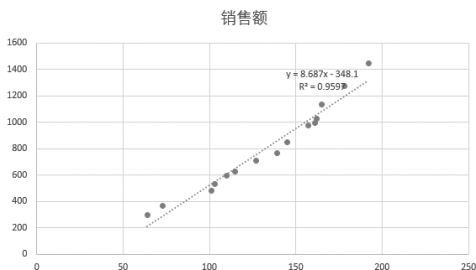
图7-37 销售额散点图及趋势线
【结论】
销售额与广告投入对应的一元线性回归方程即为y=8.687x-348.1,其中拟合度R 2=0.959 7。
【方法2:散点图法构建指数回归方程】
步骤(1)~(4)同【方法1:散点图法构建线性回归方程】
(5)在设置趋势线格式中,选择“指数”;趋势线名称设置为“散点图分析法”;选中“显示公式”和“显示R平方值”复选框,如图7-38所示。

图7-38 设置趋势线格式
(6)在散点图中,出现线性趋势线和指数回归方程:
y=149.47e0.012x
其中R 2=0.991 8,如图7-39所示。
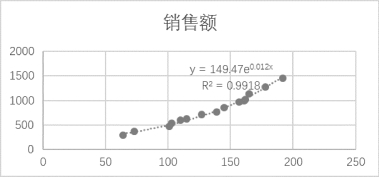
图7-39 线性趋势线与回归方程
【结论】
销售额与广告投入对应的一元指数回归方程即为y=149.47e0.012x,其中拟合度R 2=0.991 8。
实验方法1和方法2比较,指数回归方程的拟合度优于线性回归方程,但是由于散点图方法的局限性,我们只能看到拟合度一个指标,因此下面我们单击用Excel提供的回归工具进行更加详细的分析。
【方法3:利用回归工具构建线性回归方程】
(1)选择“数据”选项卡,然后单击“分析”组的“数据分析”工具中的“回归”,如图7-40所示。
图7-40 数据分析回归工具
(2)设置“回归”参数,如图7-41所示。
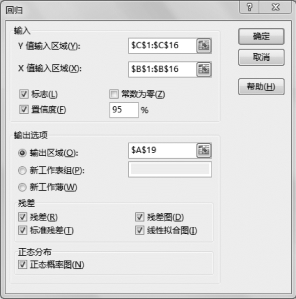
图7-41 回归工具参数设置
•Y值输入区域:$C$1:$C$16,单击实际数据区域。
•X值输入区域:$B$1:$B$16,单击实际数据区域。
•标志:√,根据输入区域是否包含标题行单击。
•置信度:95%,根据实验要求输入。
•输出区域:$A$19。这里可自行单击。
•残差:√。
•残差图:√。
•标准残差:√。
•线性拟合图:√。
•正态概率图:√。(https://www.daowen.com)
(3)回归分析结果如图7-42所示。
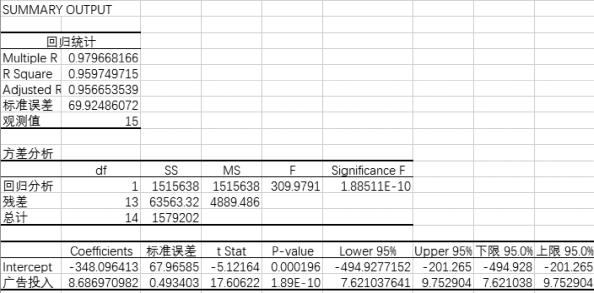
图7-42 回归分析结果
【结论】
(1)根据回归统计表可以得到相关系数为0.979 668 166,说明广告投入与销售额显著性相关,呈线性正相关关系。
(2)根据回归统计表可以得到估计的标准误差为69.92。
(3)根据回归统计表可以得到拟合度为95.97%,表明总误差平方和中有95.97%可以由回归方程来解释。
(4)根据回归的汇总输出可以得到线性回归方程为
y=8.687x-348.1
(5)Intercept对应的P值为0.000 196<0.05,表明该常数项对回归方程的影响统计上显著。
(6)“广告投入”对应的P值为1.89×10-10<0.05,表明该“广告投入”的系数对回归方程的影响统计上显著。
【方法4:利用回归工具构建指数回归方程】
Excel提供的回归工具只能构建线性方程,如果要利用回归工具构建指数回归方程,那么必然要对因变量和自变量进行一定的数学变换,形成线性关系。
假设题设的广告投入X和销售额Y存在指数关系,即
y=a e b
那么等号两边同时取对数,可以得到
ln y=bx+ln a
下面开始具体的实验步骤。
(1)选中单元格D2,输入“=LN(C2)”,并向下复制单元格。
(2)选择“数据”选项卡,然后单击“分析”组的“数据分析”工具中的“回归”。
(3)设置“回归”参数,如图7-43所示。
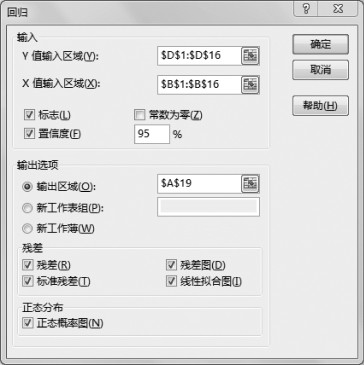
图7-43 回归参数设置
•Y值输入区域:$D$1:$D$16,单击实际数据区域。
•X值输入区域:$B$1:$B$16,单击实际数据区域。
•标志:√,根据输入区域是否包含标题行单击。
•置信度:95%,根据实验要求输入。
•输出区域:$A$19。这里可自行单击。
•残差:√。
•残差图:√。
•标准残差:√。
•线性拟合图:√。
•正态概率图:√。
(4)回归分析结果如图7-44所示。
(5)任意选一个单元格,输入“=EXP(B35)”或者“=EXP(5.0070837)”,计算出a=149.467 7,如图7-45所示。
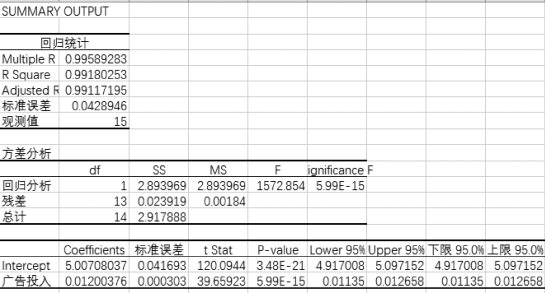
图7-44 回归结果分析
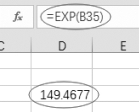
图7-45 指数函数还原原函数
【结论】
(1)根据回归统计表可以得到相关系数为0.995 892 83,说明广告投入与销售额显著性相关,呈线性正相关关系。
(2)根据回归统计表可以得到估计的标准误差为0.042 894 6。
(3)根据回归统计表可以得到拟合度为0.991 802 53,表明总误差平方和中有99.18%可以由回归方程来解释。
(4)根据回归的汇总输出可以得到指数方程对应的线性回归方程为
ln y=0.012x+5.007
对应的指数方程为
y=149.47e0.012x
(5)Intercept对应的P值为3.48×10-21<0.05,表明该常数项对回归方程的影响统计上显著。
(6)“广告投入”对应的P值为5.99×10-15<0.05,表明该“广告投入”的系数对回归方程的影响统计上显著。
【线性回归方程和指数回归方程的比较】
利用回归工具构建线性回归方程和指数回归方程的过程中,我们可以比较得到:
(1)线性回归方程的标准误差为69.92,而指数回归方程的误差e0.042 894 601=1.044,即指数回归方程的误差远低于线性回归方程的标准误差。
(2)根据回归统计表可以得到线性回归方程拟合度为95.97%,而指数回归方程的拟合度为0.991 802 53,同样也是只是指数回归方程的拟合程度更好。
