4.2.1　均已知的两个总体均值差μ1-μ2的置信区间

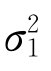
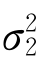4.2.1　 均已知的两个总体均值差μ1-μ2的置信区间

由附录均已知的情况下,满足正态分布,

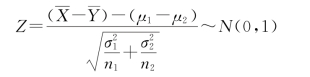
那么μ1-μ2的一个置信水平为1-α的置信区间为

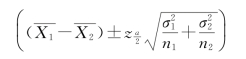
例4.5 某商店需界定两个商品的重量差别。假设两个商品的重量均服从正态分布,已知A商品的重量标准差为0.06,B商品的重量标准差为0.03,抽取100个商品进行比较,得到A商品的平均重量为52,B商品的平均重量为48,求两个商品平均重量之差在95%置信水平下的区间估计。

【实验步骤】

(1)单击单元格B8,均值差为“=B4-C4”,如图4-20所示。

(2)单击单元格B9,zα/2为“=NORM.S.INV(B6/2)”,如图4-21所示。

(3)单击单元格B11,置信区间上限为“=B8-B9*SQRT(B2 2/C2+C2 2/B2)”,如图4-22所示。单击单元格B12,置信区间下限为“=B8+B9*SQRT(B2 2/C2+C2 2/B2)”,如图4-23所示。

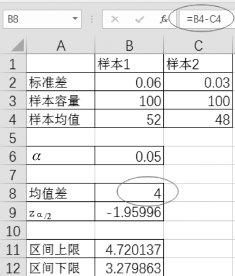
图4-20　求均值差

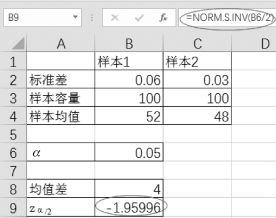
图4-21　求标准正态分布的反函数

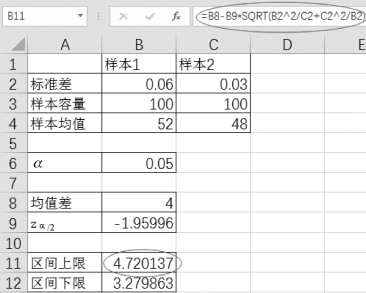
图4-22　求区间上限

【结论】两个商品平均重量之差置信水平为0.95的置信区间为(3.28,4.72)。也就是说,以此区间中的任意一个值作为μ1-μ2的近似值,其误差不大于1.44,这个误差估计的可信程度为95%。

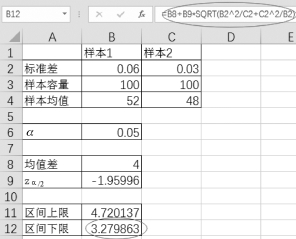
图4-23　求区间下限