4.3 (0,1)分布参数的区间估计
2026年01月15日
4.3 (0,1)分布参数的区间估计
(0,1)分布的总体X的分布律如表4-1所示。
表4-1 (0,1)分布的总体X的分布律

中心极限定理:当样本容量n较大时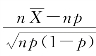 近似地服从标准正态分布N(0,1)。那么,p的一个近似的置信水平为1-α的置信区间为(p 1,p 2)。其中
近似地服从标准正态分布N(0,1)。那么,p的一个近似的置信水平为1-α的置信区间为(p 1,p 2)。其中
![]()
此处![]()
例4.8 随机抽取100个某商品,测得60个一级品,求在95%置信水平下这批商品一级品率p的置信区间。
【实验步骤】
(1)单击单元格B7,样本均值为“=B3/B2”,如图4-34所示。
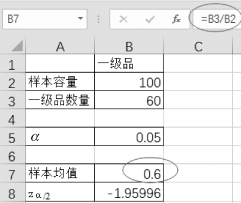
图4-34 求样本均值
(2)单击单元格B8,zα/2为“=NORM.S.INV(B5/2)”,如图4-35所示。
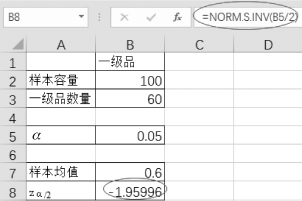
图4-35 求zα/2(https://www.daowen.com)
(3)单击单元格B10,a为“=B2+B8 2”,如图4-36所示。选择单元格B11,b为“=-(2*B2*B7+B8 2)”,如图4-37所示。选择单元格B12,c为“=B2*B7 2”,如图4-38所示。
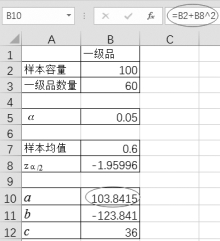
图4-36 求a
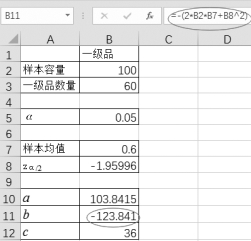
图4-37 求b
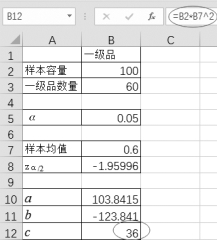
图4-38 求c
(4)单击单元格B14,置信区间下限p 1为“=(-B11-SQRT(B11 2-4*B10*B12))/2/B10”,如图4-39所示。
(5)单击单元格B15,置信区间上限p 2为“=(-B11+SQRT(B11 2-4*B10*B12))/2/B10”,如图4-40所示。
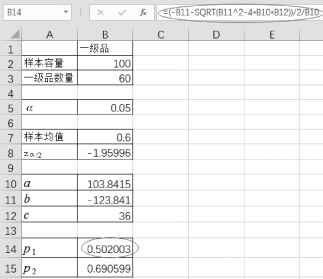
图4-39 求p 1
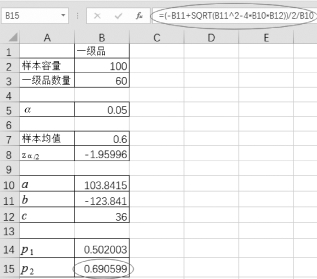
图4-40 求p 2
【结论】该商品一级品率在置信水平为0.95的置信区间为(0.50,0.69)。
