8.3 移动平均法
移动平均,又称“移动平均线”,简称均线,是统计分析中一种分析时间序列数据的工具。移动平均法是测定时间序列长期趋势的基本方法,其基本原理是对时间序列按照一定的项数逐项移动计算平均值,从而达到对原始数据序列修正、消除偶然因素的目的。数学上,移动平均可视为一种卷积。统计中的移动平均法是对动态数列的修匀的一种方法,其本质就是将动态数列的时距扩大。时距扩大法是计算扩大时距内时期数值的和,而移动平均是采用逐期推移的简单算术平均法,计算出扩大时距的各个平均值,这一些值的推移动态平均数就形成了一个新的数列,即移动平均序列。通过移动平均,现象短期不规则变动的影响被消除。如果扩大的时距能与现象周期波动的时距相一致或为其倍数,就能进一步削弱季节变动和循环变动的影响,更好地反映现象发展的基本趋势。
移动平均法是一种简单平滑预测技术,使用移动平均法进行预测能平滑掉需求的突然波动对预测结果的影响,适用于即期预测。当产品需求既不快速增长也不快速下降,且不存在季节性因素时,移动平均法能有效地消除预测中的随机波动,是非常有用的。当时间序列的数值由于受周期变动和随机波动的影响,起伏较大,不易显示出事件的发展趋势时,使用移动平均法可以消除这些因素的影响,显示出事件的发展方向与趋势,然后依趋势线分析预测序列的长期趋势。
移动平均法分为简单移动平均法和加权移动平均法。
1.简单移动平均法
简单移动平均的各元素的权重都相等。简单移动平均的计算公式如下:
![]()
其中:F t表示对下一期的预测值;n表示移动平均的时期个数;A t-i表示前i期的实际值。
2.加权移动平均法
加权移动平均给固定跨越期限内的每个变量值以不相等的权重。其原理是:历史各期产品需求的数据信息对预测未来期内的需求量的作用是不一样的。除了以n为周期的周期性变化外,远离目标期的变量值的影响力相对较低,故应给予较低的权重。
加权移动平均法的计算公式如下:(https://www.daowen.com)
![]()
其中:w i表示第t-i期实际销售额的权重;n表示移动平均的时期个数;这里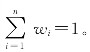
在运用加权平均法时,权重的选择是一个应该注意的问题。经验法和试算法是选择权重的最简单的方法。一般而言,最近期的数据最能预示未来的情况,因而权重应大些。例如,根据前一个月的利润和生产能力比起根据前几个月能更好地估测下个月的利润和生产能力。但是,如果数据是季节性的,则权重也应是季节性的。移动平均法对原序列有修匀或平滑的作用,使得原序列的上下波动被削弱了,而且平均的时距项数n越大,对数列的修匀作用越强。当序列包含季节变动时,移动平均时距项数n应与季节变动长度一致,才能消除其季节变动;当序列包含周期变动时,平均时距项数n应和周期长度基本一致,才能较好地消除周期波动。
但移动平均法运用时也存在着如下问题:
①加大移动平均法的期数(即加大n值)会使平滑波动效果更好,但会使预测值对数据实际变动更不敏感。
②移动平均值并不能总是很好地反映出趋势。由于是平均值,预测值总是停留在过去的水平上而无法预计会导致将来更高或更低的波动。
③移动平均法要有大量的过去数据的记录。
④它通过引进愈来愈近的新数据,不断修改平均值,以之作为预测值。
下面着重介绍两种常用的移动平均方法:中心移动平均与历史移动平均。
