5.2.2 方差未知条件下单个正态总体均值的假设检验
总体的标准差未知的条件下,用能计算出来的样本的标准差S来代替未知的总体标准差,新的统计量服从自由度为n-1的t分布:
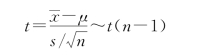
需要注意的是,在实际应用中,当总体标准差未知时,一般考虑,小样本满足t分布,大样本近似满足正态分布。
1.方差未知且为小样本情况下总体均值的双侧检验
双侧检验是指检验时拒绝域在数据分布的两侧,Excel 2019提供T.DIST.2T函数返回学生的双尾t分布,T.INV.2T函数返回学生t分布的双尾反函数(函数详细介绍见2.3.2节)。
例5.3 已知货物的质量服从正态分布但方差未知,现从中随机抽取20件商品,质量如表5-3所示,试分别用临界值法和P值法判断能否在0.1的显著性水平下认为商品的平均质量为110 kg。
表5-3 20件样品质量(单位:kg)
【临界值法步骤】
按照题意检验假设
H 0:μ=μ0=110;H 1:μ≠μ0
这是一个双侧检测问题,临界值法解答过程如下:
(1)单击单元格B9,计算平均值为“=AVERAGE(A2:E5)”,结果为111.437 5。
(2)单击单元格B10,计算样本标准差为“=STDEV.S(A2:E5)”,如图5-6所示。
(3)单击单元格B15,计算统计量的值“=ABS(B10-B8)/(B11/SQRT(B7))”,结果为0.969 208 194。
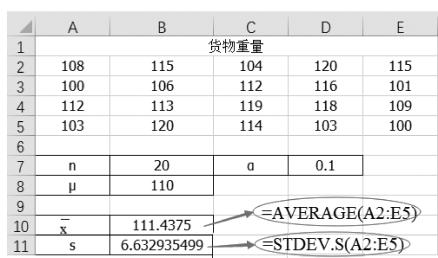
图5-6 计算样本均值和样本标准差
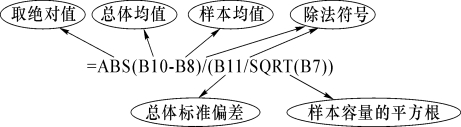
(4)单击单元格B16,计算临界值“=ABS(T.INV.2T(D7,B7-1))”,结果为2.093 024 054。
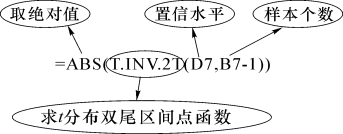
(5)单击单元格B17,得到假设检验的结论“=IF(B15＜B16,"接受H0:μ=110","接受H1:μ≠110")”,即假如样本值的绝对值小于临界值的绝对值,那么接受原假设H 0:μ=μ0=110,否则接受备择假设H 1:μ≠μ0。最后显示结果为接受H 0:μ=μ0=110,如图5-7所示。
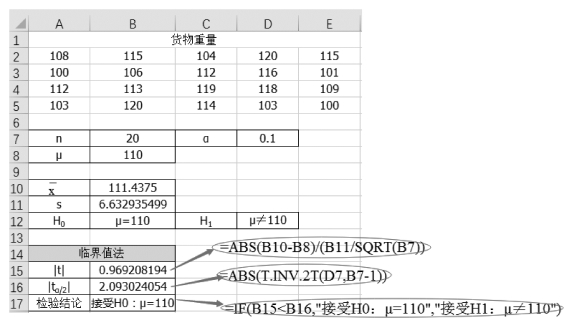
图5-7 临界值法的结论
临界值法解决问题思路比较清晰,更容易被理解,但是用P值法解决更加简单和明确,因此P值法更加常用。
【P值法步骤】
(1)单击单元格B21,计算概率的值“=1-T.DIST.2T(B20,B7-1)”,如图5-8所示。
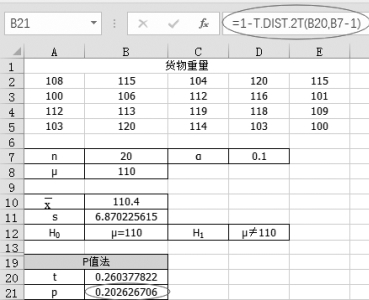
图5-8 计算统计量对应的概率值
(2)单击单元格B22,得到假设检验的结论“=IF(B21＞D7,"接受H0:μ=110","接受H1:μ≠110")”,如图5-9所示。
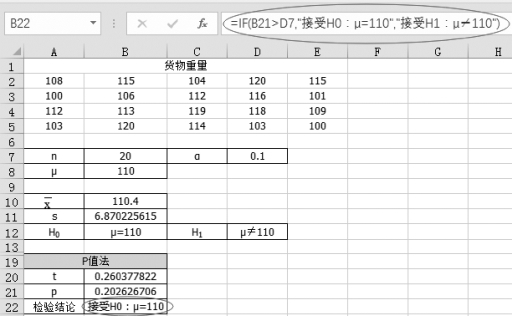
图5-9 P值法的结论
【结论】
无论是临界值法还是P值法,都得到相同的结论:在0.1的显著性水平下认为商品的平均质量为110 kg。
2.方差未知且为小样本下总体均值的单侧检验
单侧检验是指检验时拒绝域在数据分布的单侧,Excel 2019提供T.DIST函数返回学生的左尾t分布,T.DIST.RT函数返回学生的右尾t分布,以及T.INV函数返回学生的t分布的左尾反函数。
例5.4 已知小学生每月的图书消费额服从正态分布,现从中随机抽取25名学生的月消费额,如表5-4所示,试分别采用两种方法判断能否在0.05的显著水平下认为学生每月图书消费额不低于50元。
表5-4 大学生每月图书消费抽样(单位:元)
【临界值法步骤】
按照题意检验假设
H 0:μ≥μ0=50;H 1:μ＜μ0
这是左尾检测问题,临界值法解答过程如下:
(1)单击单元格B9,计算平均值为“=AVERAGE(A2:E5)”,结果为50.208 3。
(2)单击单元格B10,计算样本标准差为“=STDEV.S(A1:F4)”,结果为6.121 8,如图5-10所示。
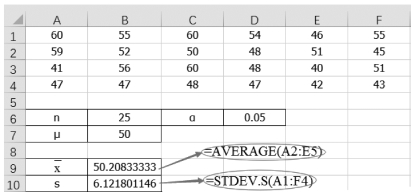
图5-10 计算样本均值的样本标准差
(3)单击单元格B14,计算统计量t为“=(B9-B7)/(B10/SQRT(B6))”,结果为0.170 2,如图5-11所示。
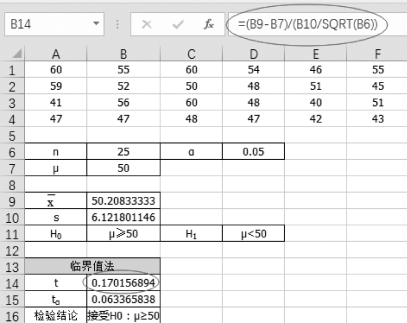
图5-11 计算统计量 t 的值
(4)单击单元格B15,计算临界值tα为“=T.INV(1-D6,B6-1)”,结果为1.701 9,如图5-12所示。
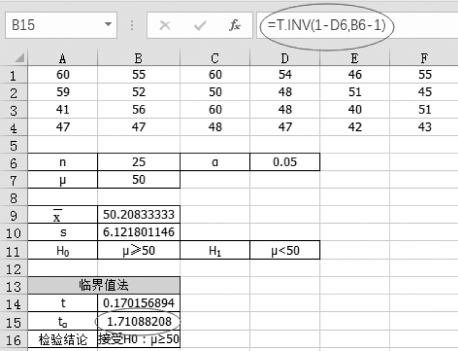
图5-12 计算t临界值
(5)单击单元格B16,得到假设检验的结论“=IF(B14＜-B15,"接受H1:μ＜50","接受H0:μ≥50")”,如图5-13所示。
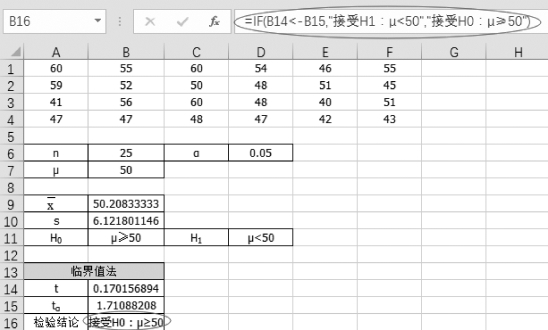
图5-13 临界值法的结论
【P值法步骤】
(1)单击单元格B20,计算概率的值“=T.DIST(B19,B6-1,1)”,如图5-14所示。
(2)单击单元格B21,得到假设检验的结论“=IF(B20＜D6,"接受H1:μ＜50","接受H0:μ≥50")”,如图5-15所示。
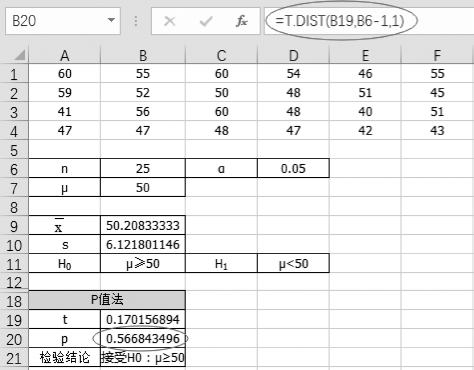
图5-14 计算统计量对应的概率值
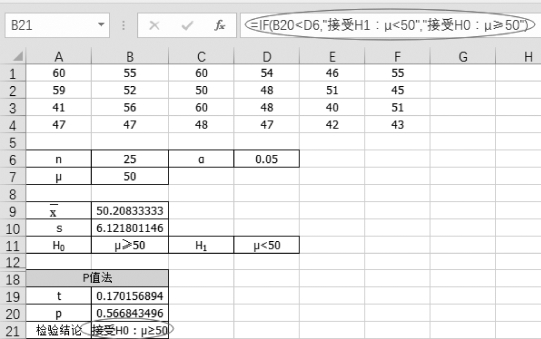
图5-15 P值法的结论
【结论】
无论是临界值法还是P值法,都得到相同的结论:在0.05的显著性水平下,无法拒绝学生每月图书消费额不低于50元。
3.方差未知且为大样本情况下总体均值的单侧检验
在总体方差未知的情况下,当样本容量n＞30,即为大样本时,可用正态分布来近似代替t分布。无论方差是否可知,根据中心极限定理,只要抽取样本足够大,抽样分布就会服从正态分布。
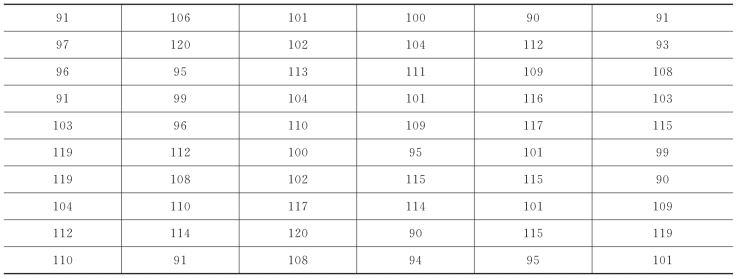
例5.5 某厂家对其生产商品的平均质量进行检验,面粉质量的总体方差未知,随机抽取60箱样本称重后结果如表5-5所示,试在0.05的显著性水平下判断该仓库中面粉平均质量是否为105 kg。
表5-5 某商品60箱样本质量(单位:kg)
【临界值法步骤】
按照题意检验假设
H 0:μ=μ0=105;H 1:μ≠μ0
这是双尾检测问题,临界值法解答过程如下:
(1)单击单元格B15,计算平均值为“=AVERAGE(A1:F10)”,结果为105.033。
(2)单击单元格B16,计算样本标准差为“=STDEV.S(A1:F10)”,结果为9.102,如图5-16所示。
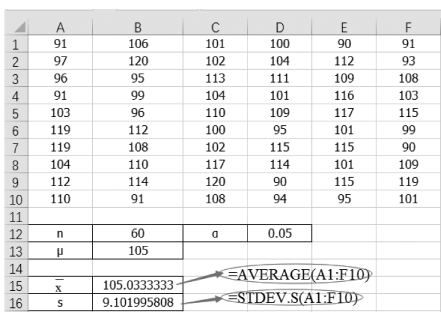
图5-16 计算样本均值与样本标准差
(3)单击单元格B19,计算统计量
为“=ABS(B15-B13)/(B16/SQRT(B12))”,结果为0.0284。
(4)单击单元格B20,计算临界值
为“=ABS(NORM.S.INV(D12/2))”,结果为1.96,如图5-17所示。
(5)单击单元格B21,得到检验结论“=IF(B19＜B20,"接受H0:μ=105","接受H1:μ≠105")”,如图5-18所示。
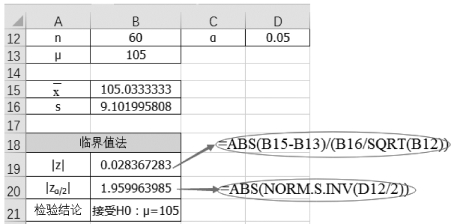
图5-17 计算z值与临界值
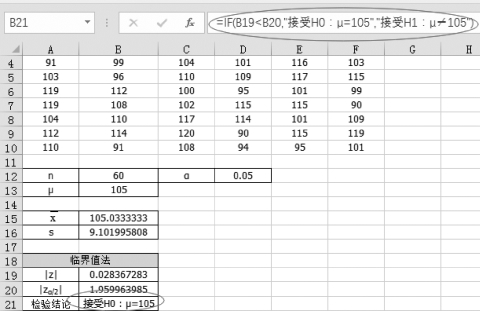
图5-18 临界值法的结论
【P值法步骤】
(1)单击单元格B25,计算概率的值“=MIN(Z.TEST(A1:F10,B13),1-Z.TEST(A1:F10,B13))”,如图5-19所示。
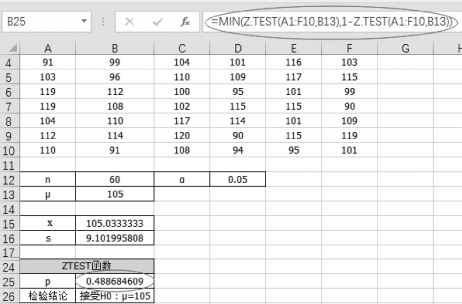
图5-19 计算统计量对应的概率
(2)单击单元格B26,得到检验结论“=IF(B25＞D12/2,"接受H0:μ=105","接受H1:μ≠105")”,如图5-20所示。
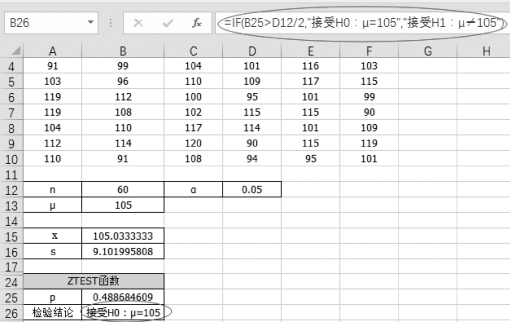
图5-20 P值法的结论
【结论】
无论是临界值法还是P值法,都得到相同的结论:在0.05的显著性水平下,判断该仓库中面粉平均质量不否认为105 kg。