3.1.3 抽样的综合方法
总体单位数N较大或者总体各单元之间差异较大时,如果采用简单随机抽样对总体指标进行估计,通常会产生很大的误差。因此在实际抽样中总体数较多时,可将总体分成均衡的几个部分,然后按照预先定出的规则,从每一部分抽取某些个体得到所需要的样本,或者直接抽取一部分将其全部作为样本。
下面介绍几种常见的抽样方法。
1.等距抽样
等距抽样是最接近于简单抽样的一种系统抽样方法。如果抽出的单位在总体中是均匀分布的,且抽取样本可少于纯随机抽样,那么就可以选择等距抽样。
等距抽样首先根据样本容量选取样本间隔或周期,将总体划分成若干大小相同的区间。然后在第一个区间利用简单随机抽样选取样本起点,后面所有的样本都是根据样本间隔或周期选取。换句话说,只有第一个区间采用了随机抽样,而后面所有的样本是由第一个样本和样本间隔确定的。
等距抽样方式相对于简单随机抽样方式最主要的优势就是经济性。等距抽样方式比简单随机抽样更为简单,花的时间更少,并且花费也少,而且等距抽样得到的样本几乎与简单随机抽样得到的样本是相同的。因此在定量抽样调查中,等距抽样常常代替简单随机抽样,应用普遍。
等距抽样的一般步骤如下。
步骤1:将总体划分成n个区间,计算对应的每个区间的样本个数Q。

步骤2:采用简单随机抽样,抽取1~Q之间的随机样本R。选取样本数可以采取简单随机抽样中的任意方法。
步骤3:抽取所有的样本,样本编号依次为R,Q+R,Q+2R,…
这里需要注意的是总体单位的排列。一方面,一些总体单位数可能包含隐蔽的形态或者是“不合格样本”,等距抽样把它们抽选为样本,有可能会造成较大偏差。另一方面,等距抽样要防止周期性偏差,因为它会降低样本的代表性。例如,军队人员名单通常按班排列,10人一班,班长排第1名,若抽样距离也取10时,则样本或全由士兵组成或全由班长组成。因此,等距抽样要求数据无规律性,不能存在固定间隔,否则会影响抽样的准确性。进行等距抽样时,必须充分利用已有信息对总体单位进行排队后再抽样,从而提高抽样效率。
按照具体实施等距抽样的做法,等距抽样可分为直线等距抽样、对称等距抽样和循环等距抽样。等距抽样的系统抽样方法可分为间隔定时法、间隔定量法、分部比例法。
下面通过具体的例题来看等距抽样的应用。
例3.6 某学院有学生812人(假设该学校的学生编号从1~812),要选择20名同学参加某调研活动,为了数据的真实性并提高抽样效率,该学校采取等距抽取的方式随机抽取出参加调研的同学。
【实验步骤】
步骤1:将总体划分成20个区间,计算每个区间的样本数,在单元格B4中,输入“=ROUND(B1/B2,0)”,如图3-21所示。
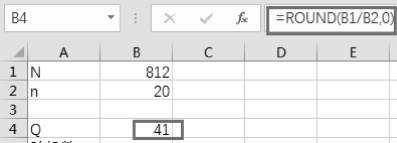
图3-21 计算区间的样本数
步骤2:利用RANDBETWEEN函数抽取第一个区间内的随机数,在单元格B5中,输入“=RANDBETWEEN(1,$B$4)”,如图3-22所示。
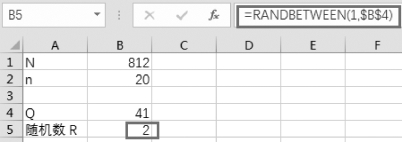
图3-22 利用RANDBETWEEN 函数对第一个区间进行简单随机抽样
步骤3:将B5的结果选择性粘贴到单元格B7中,只粘贴“数值”;
步骤4:在单元格B8中输入“=B7+$B$4”,如图3-23所示,即计算第二个区间内的样本号,区间长度加上抽取的随机数。
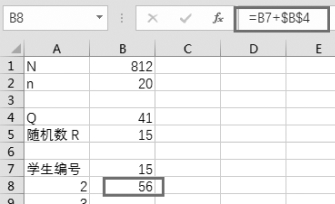
图3-23 计算第二个区间的抽样编号
步骤5:在单元格B9~B26中,复制B8的公式,如图3-24所示,即为所得。
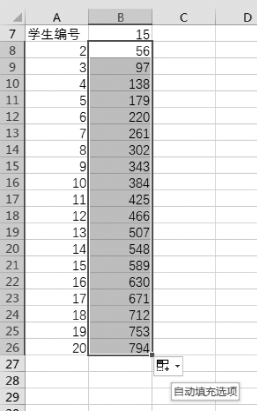
图3-24 计算3-20个区间的抽样编号
2.分层抽样
分层抽样,又称为类型抽样或分类抽样,即抽样在每个层中独立进行,总的样本由各层样本构成。(https://www.daowen.com)
总体是由差异明显的几个部分组成时,往往选用分层抽样的方法。分层抽样的特点是同一层中各单位差异小,而不同层之间的差异大。从每一层中抽取样本,这样样本就有该层的代表性,将每一层的样本集合起来,就组成了所有样本。使用分层抽样可以提高估计的精度,也便于依托各级管理机构进行组织和实施。
分层抽样尽量利用事先所掌握的各种信息,并充分考虑保持样本结构与总体结构的一致性,这对提高样本的代表性非常重要。
分层抽样需要注意两个问题。
(1)需选择合适的分层方法,保证每层个体差异小,而层与层之间差异较大。
(2)每一层样本数由该层个体数、总样本容量与总体个体数的比例确定。例如,总样本数为N,样本容量为n,该层个体数为N i,那么该层样本数
![]()
具体来说,分层抽样的步骤如下。
步骤1:根据已经掌握的信息,将总体分成互不相交的m个层。
步骤2:根据总体的个体数N和样本容量n计算抽样比k=n/N。
步骤3:确定每一层应抽取的个体数目,并使每一层应抽取的个体数目之和为样本容量n。
步骤4:按步骤3确定的数目在各层中随机抽取个体,合在一起得到容量为n的样本。
例3.7 某城市有210家百货商店,其中大型商店20家,中型商店40家,小型商店150家。为了掌握各商店的营业情况,计划抽取一个容量为21的样本,按照分层抽样方法抽取时,各种百货商店分别要抽取多少家?
【解题步骤】
步骤1:根据题意,该城市的百货商店分为3层:大型商店、中型商店和小型商店。
步骤2:计算抽样比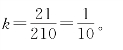
步骤3:分别计算3层的样本数:
•大型商店的抽样个数为![]()
•中型商店的抽样个数为![]()
•小型商店的抽样个数为![]()
步骤4:计算整体样本数n=n 1+n 2+n 3=2+4+1=21。
步骤5:每一层分别进行简单随机抽样。
3.整群抽样
整群抽样是指整群地抽选样本单位,对被抽选的群进行全面调查的一种抽样组织方式。例如,调查中学生患近视的情况,抽取某一个班做统计;进行产品检验;每隔8 h抽1 h生产的全部产品进行检验等。
整群抽样的实施步骤如下。
先将总体分为i个群,然后从i个群中随机抽取若干个群,对这些群内所有个体或单元均进行调查。抽样过程可分为以下几个步骤:
(1)确定分群的标注;
(2)总体N分成若干个互不重叠的部分,每个部分为一群;
(3)据各样本量,确定应该抽取的群数;
(4)采用简单随机抽样或系统抽样方法,从i个群中抽取确定的群数。
整群抽样与分层抽样在形式上有相似之处,但实际上差别很大。分层抽样要求各层之间的差异很大,层内个体或单元差异小,而整群抽样要求群与群之间的差异比较小,群内个体或单元差异大。分层抽样的样本是从每个层内抽取若干单元或个体构成,而整群抽样则是要么整群抽取,要么整群不被抽取。
