4.2.4 系统建模的主要理论与方法
一切事物皆有其运动特征和发展规律,因而要求系统工程人员在建造系统模型时,要根据不同的研究对象,采用不同的理论和方法。主要的建模理论有:“黑箱”理论、“白箱”理论、“灰箱”理论等。常用的建模方法有推理法、实验法、统计分析法、类似法和混合法五种。
4.2.4.1 推理法
利用已知的定律和定理,经过一定的分析和推理得到系统模型。这个方法适用于大多数的工程系统或称“白箱”系统(系统内部结构和特性比较清楚)。推理法可以表达为下面的简洁形式:
(1)对象 比较简单的“白箱”系统。
(2)方法 利用自然科学的各种定理、定律(如物理、化学、数学、电学的定理、定律)和社会科学的各种规律(如经济规律),经过一定的分析和推理,可以得到系统的数学模型。
[举例] 安排生产优化的数学模型
某化工厂生产A、B两种产品,已知:生产A产品1kg需耗煤9t、电力4000度和3个劳动日,可获利700元;生产B产品1kg需耗煤4t、电力5000度和10个劳动日,可获利1200元。因条件限制,这个厂只能得到煤360t,电力20万度和劳动日300个。问:如何安排生产(即生产A、B产品各多少?)才能获利最多,请建立解决此问题的数学模型。
解:这是在一定条件求极值的生产管理问题,可运用运筹学中的线性规划方法建立线性规划模型。先将给出的数据整理成表4-2。
表4-2 数据整理表
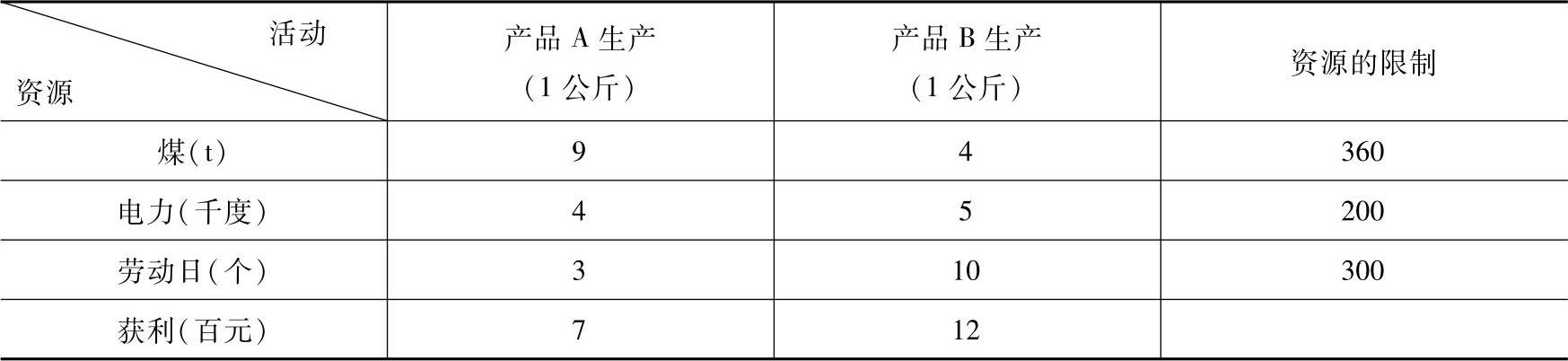
设生产A、B产品各为x1、x2公斤,则此问题变为求x1和x2满足下列条件:

使得总获利最大:
max7x1+12x2 (b)
显然(a)为约束条件,(b)为目标函数,这是一个典型的线性规划模型。
4.2.4.2 实验法
通过试验方法测量其输入输出,然后按照一定的辨识方法得到系统模型。这个方法适用于“黑箱”或“灰箱”的系统(系统内部结构和特性不清楚或模糊)。通过实验,找出系统的输入和输出数据,然后运用自动控制理论中的传递函数方法或其他的数学方法(如回归分析、时序分析等方法),建立系统输出与输入之间的关系——系统的数学模型。车辆结构的模态参数识别就是通过所述的试验方法,先获取传递函数,然后通过频响函数拟合,获取模态参数。
4.2.4.3 统计分析法
那些属于“黑箱”的系统,但又不允许直接进行试验观察的系统,可以采用数据收集和统计分析的方法来建造系统模型。该方法也称为数据拟合法。适用于非工程类系统。
常用的“拟合曲线”有以下几种:直线型、对数函数型、幂函数型、指数函数型和多项式型。
4.2.4.4 类似法
利用结构和性质的相似性,建造原系统的类似模型。例如很多机械系统、气动力学系统、水力学系统、热力学系统与电路系统之间某些现象彼此类似,特别是通过微分方程描述的动力学方程基本一致,因此可以利用成熟的电路系统来构造上述系统的类似模型。
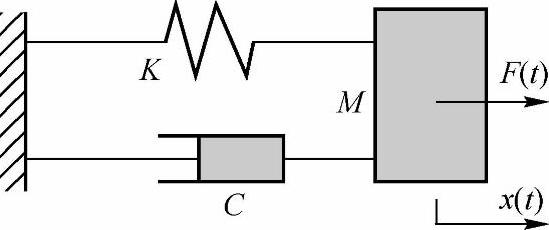
[举例] 机械系统的电路类似模型
在机械系统与电路系统分别用推理法建造出数学模型(用微分方程描述的动力学方程)以后发现,它们具有同型性(即具有相似的数学描述并在参数上一一对应,其运动也都具有振荡的特性),因此,电路系统可以认为是机械系统的一种类似模型,反之亦然。
a)机械系统
系统的数学模型(https://www.daowen.com)
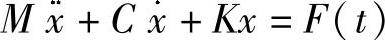
变量及参数(属性):
位移x
速度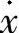
加速度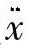
外力F(t)
质量M
阻尼系数C
弹簧刚度K
系统行为:机械振动
b)电路系统
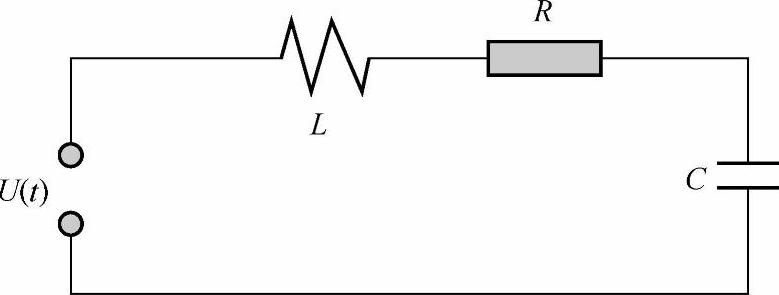
系统的数学模型
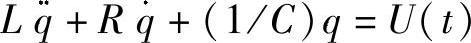
变量及参数(属性):
电荷q
电流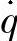
电流变化速度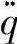
电压U(t)
电感L
电阻R
电容C
系统行为:电振荡
4.2.4.5 混合法
混合法是以上各种方法的综合使用。如果系统有多个子系统,则可以分别采用不同的建模方法,最终形成总系统模型。
