6.3.7 投入产出预测法
在经济活动中分析投入多少财力、物力、人力,产出多少社会财富是衡量经济效益高低的主要标志。投入产出技术正是一种研究经济系统各部门间的“投入”与“产出”关系的数学模型,该方法最早由美国著名的经济学家瓦·列昂捷夫(W.Leontief)在1936年提出,是目前比较成熟的经济分析方法。
投入产出法可揭示经济活动中各种资源投入与产出间数量关系,既可反映经济活动直接消耗关系,又可反映间接消耗关系;既可用于经济计划,又可用于经济预测,是研究经济问题的一种好方法。
我国20世纪60年代初期开始宣传和介绍该方法,并于1974年开始编制第一个全国性投入产出表,开始用于计划、预测工作。投入产出法已从简单初始形式发展到较复杂结构,并逐渐应用到社会科学许多领域。我国经济建设迅速发展和科学技术突飞猛进,为投入产出法提供了广阔应用前景。
1.投入产出概念
投入指的是从事一项经济活动消耗。如生产过程和运输过程中所消耗原材料、辅助材料、能源、机器设备和劳动力等。投入就是从事生产和运输活动中的投入;产出指从事经济活动结果,如一定数量的产品,或完成一定数量运输量。投入产出法研究经济系统中各子系统间投入与产出间相互关系,为经济预测、经济计划、政策模拟以及综合平衡提供依据。
2.投入产出表结构
结构用两种形式描述:
一种是用线性方程组来描述,具体的经济结构的特点由这些方程中的系数来反映,这些系数是由统计、预测或其他数学推导方法来测定;另一种是用表格来描述。见表6-15。
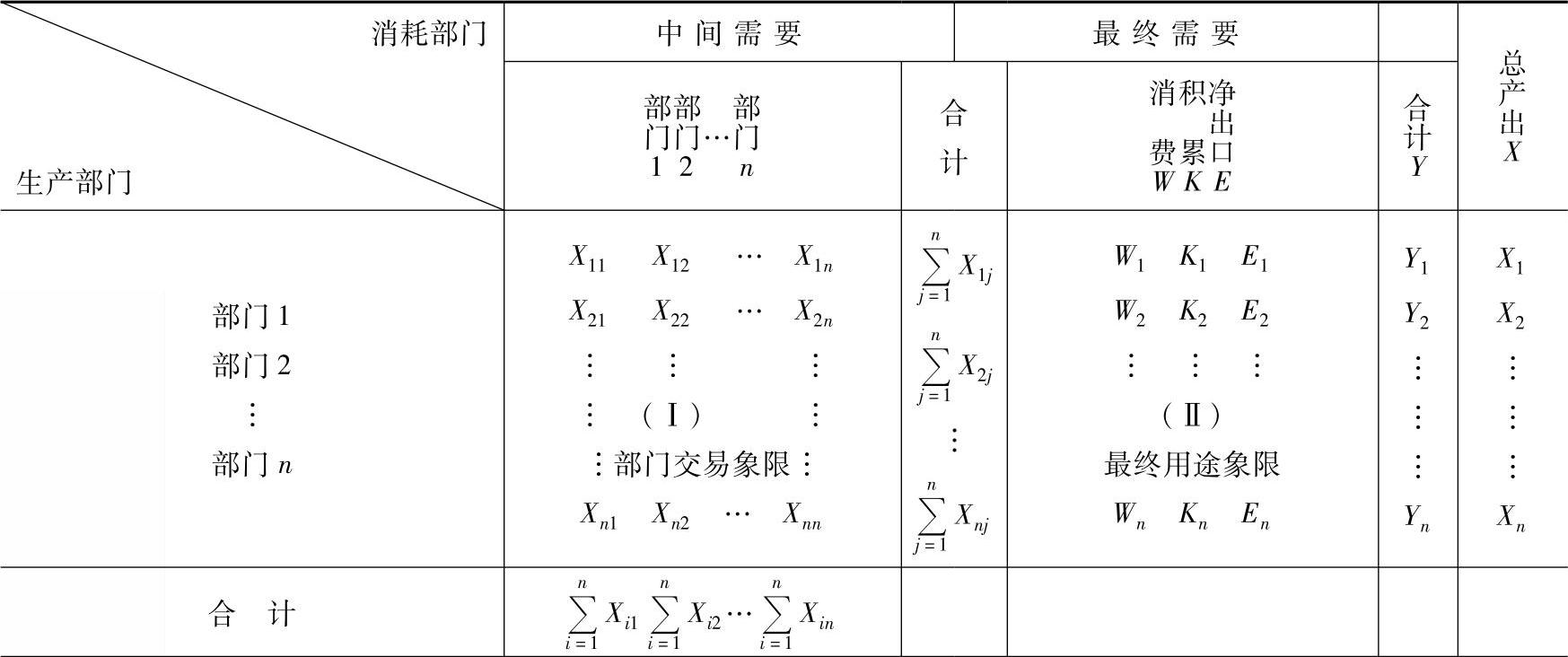
一个投入产出表包括四个象限(部分):
第Ⅰ象限:部门间交易象限或部门间流量象限:由各部门纵横交叉而成,是一个方形棋盘式平衡表,行数等于列数。其中行代表产出,列代表投入,每个部门既是投入消耗者,又是产出生产者。并巨,相同编号横行和纵列代表同名称部门。
第Ⅱ象限:最终用途象限,又称最终产品象限。这部分反映最终产品实物构成及其使用。
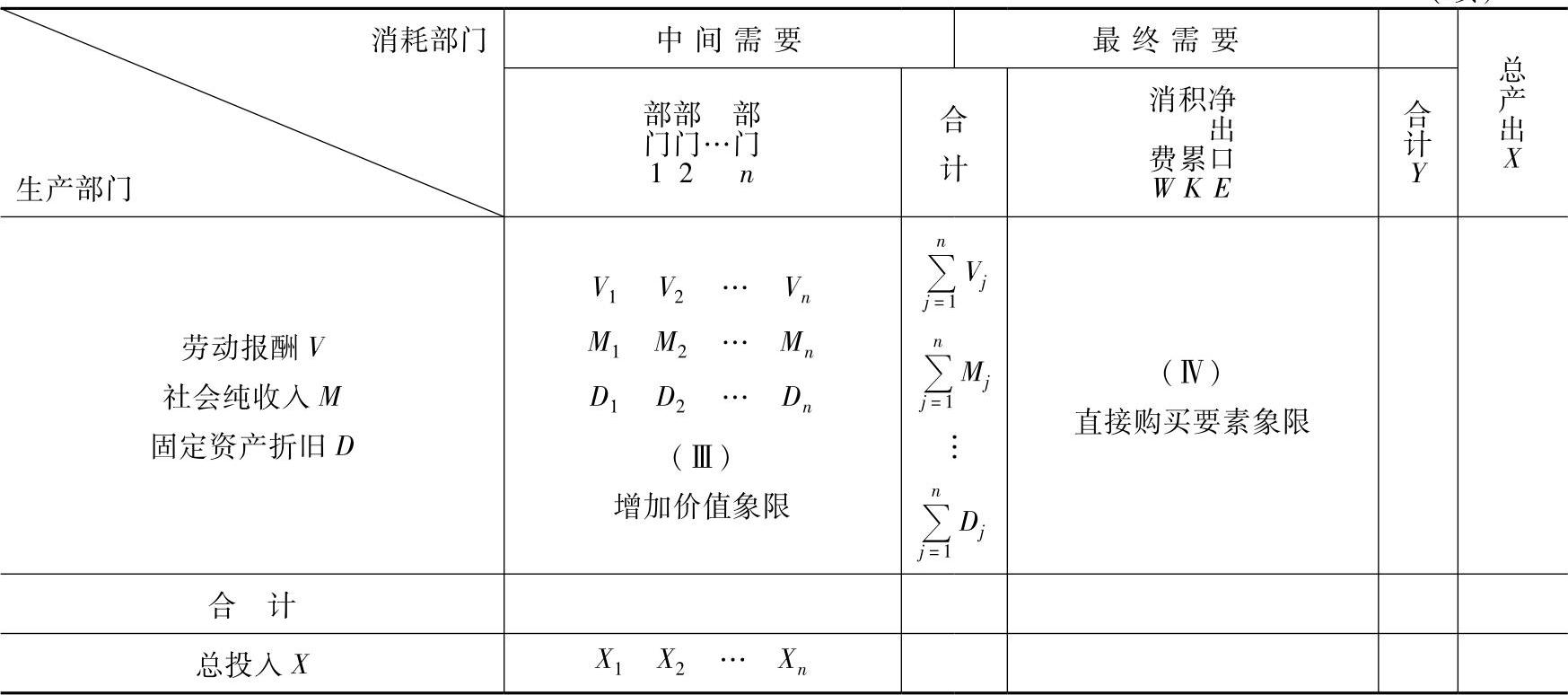
第Ⅲ象限:增加价值象限。包括:劳动报酬,如劳动者个人收入;社会纯收入,如政府税收;固定资产折旧。
第Ⅳ象限:直接购买要素象限:这一部分反映国民收入再分配。
投入产出表中的数字若为统计数字(即已经实现了的指标),则为投入产出统计表,可用来进行经济分析和政策分析。投入产出表中的数字若为预测值或计划值,则为投入产出计划表,可用来进行经济预测、政策模拟和安排生产计划等。
3.投入产出数学模型
通过编制投入产出表,运用线性代数工具建立数学模型,从而揭示国民经济各部门、再生产各环节之间的内在联系,并据此进行经济分析、预测和安排预算计划。按计量单位不同,该模型可分为价值型和实物型。
投入产出表描述了各经济部门在某个时期的投入产出情况。如表6-15中第一行中X1表示部门1的总产出水平,X11为本部门的使用量,X1j(j=1,2,…,n)为部门1提供给部门j的使用量,各部门的供给最终需求(包括居民消耗、政府使用、出口和社会储备等)为yj(j=1,2,…,n)。这几个方面投入的总和代表了这个时期的总产出水平。
表6-15 投入产出表
(续)
投入产出的基本平衡关系:
从左到右: 中间需求+最终需求=总产出 (6-86)
从上到下: 中间消耗+净产值=总投入 (6-87)
由此得产出平衡方程组(也称分配平衡方程组)
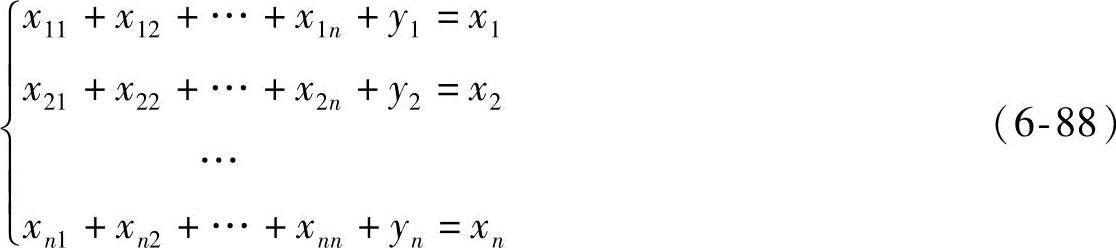
或简写成
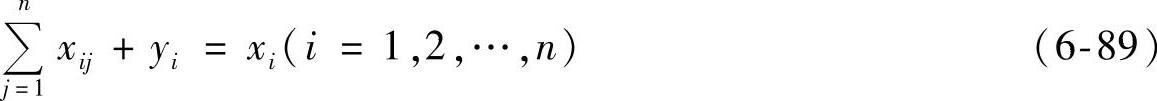
也可以把上式改写成需求平衡方程组
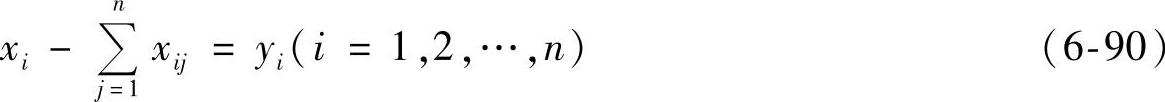
由投入产出表可以写出如下的投入平衡方程组(也称消耗平衡方程组)
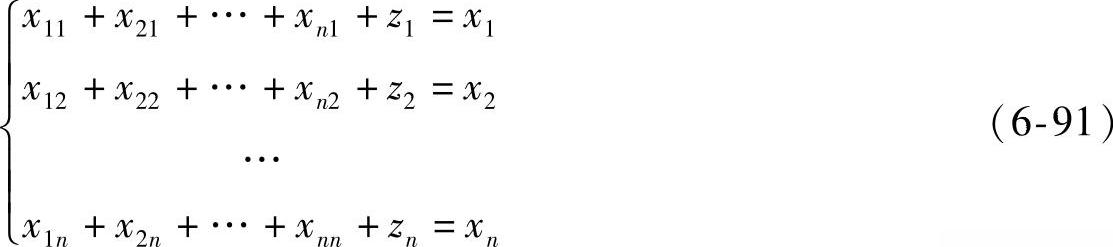
上式也可以简写为
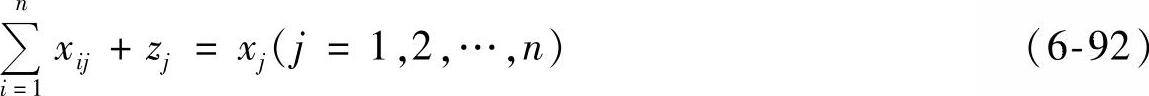 (https://www.daowen.com)
(https://www.daowen.com)
由式(6-90)和式(6-92),可得

上式表明就整个国民经济来讲,用于非生产的消费、积累、储备和出口等方面产品的总价值与整个国民经济净产值的总和相等。
(1)直接消耗系数 把第j部门生产单位价值所消耗第i部门的价值称为第j部门对第i部门的直接消耗系数,记作aij(i,j=1,2,…,n)。
由定义得

把投入产出表中的各个中间需求xij换成相应的aij后得到的数表称为直接消耗系数表,并称n阶矩阵A=(aij)为直接消耗系数矩阵。
由直接消耗系数的定义xij=aijxj代入(6-91),得
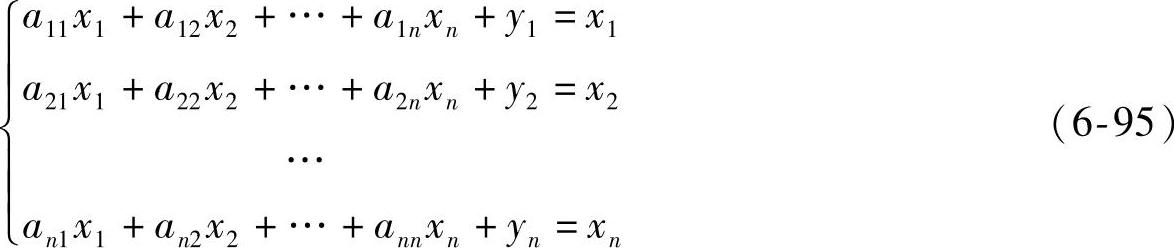
令X=(x1x2…xn)′,Y=(y1y2…yn)′
式(6-95)可表示为AX+Y=X,或
(E-A)X=Y (6-96)称X的系数矩阵E-A为列昂捷夫矩阵。
类似地把xij=aijxj代入平衡方程(6-92)得到
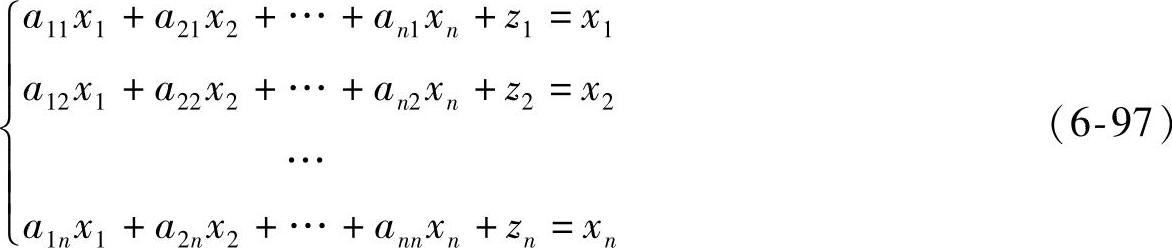
写成矩阵形式为
X=DX+Z或(E-D)X=Z (6-98)
其中
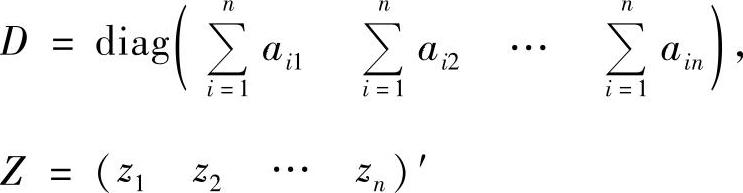
(2)完全消耗系数 直接消耗系数只反映各部门间的直接消耗,不能反映各部门间的间接消耗,为此我们给出如下定义。
设第j部门生产单位价值量直接和间接消耗的第i部门的价值量总和,称为第j部门对第i部门的完全消耗系数,记作bij(i,j=1,2,…,n)。
由bij构成的n阶方阵B=(bij)称为各部门间的完全消耗系数矩阵。
定理6.2.1 第j部门对第i部门的完全消耗系数bij满足方程
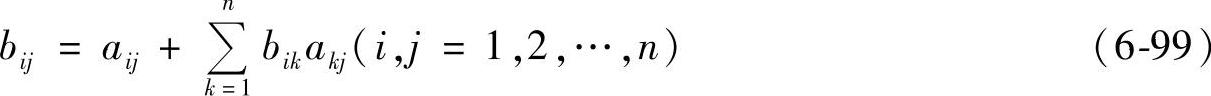
定理6.2.2 设n个部门的直接消耗系数矩阵为A,完全消耗系数矩阵为B,则有
B=(E-A)-1-E (6-100)
定理6.2.3 如果第j部门最终需求增加Δyj,而其他部门的最终需求不变,那么部门总产出X的增量为
ΔX=Δyj(Bj+ej) (6-101)
其中
ΔX=(Δx1Δx2…Δxn)′,Bj=(b1jb2j…bnj),ej为单位坐标向量
定理6.2.3表明,由第j部门最终需求的增加(其他部门的最终需求不变),引起了各部门总产值的增加。Δyj(Bj+ej)从数量上表示了各部门的增加量。如果没有这些追加,第j部门要完成增加Δyj最终需求的任务就不能实现。
4.投入产出实现模型的简单应用
投入产出法来源于一个经济系统各部门生产和消耗的实际统计资料。它同时描述了当时各部门之间的投入与产出协调关系,反映了产品供应与需求的平衡关系,因而在实际中有广泛应用。在经济分析方面可以用于结构分析,还可以用于编制经济计划和进行经济调整等。
具体做法是:根据投入产出表中的数据,算出报告期的直接消耗系数矩阵A。假定计划期同报告期的直接消耗系数是相同的,因此把A作为计划期的直接消耗系数矩阵。再按公式X=(E-A)-1Y算出总产出向量X。
