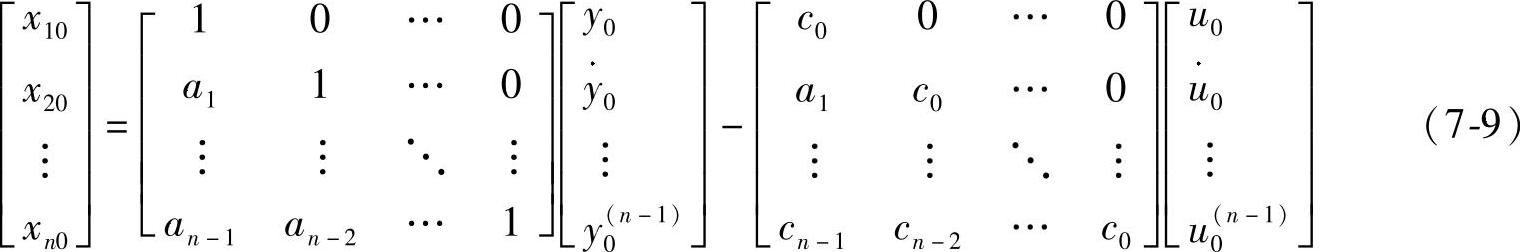7.2.1  仿真模型的建立

7.2.1 仿真模型的建立

设有一个连续系统，它的高阶微分方程数学模型如公式7-1所示

现引进n个状态变量

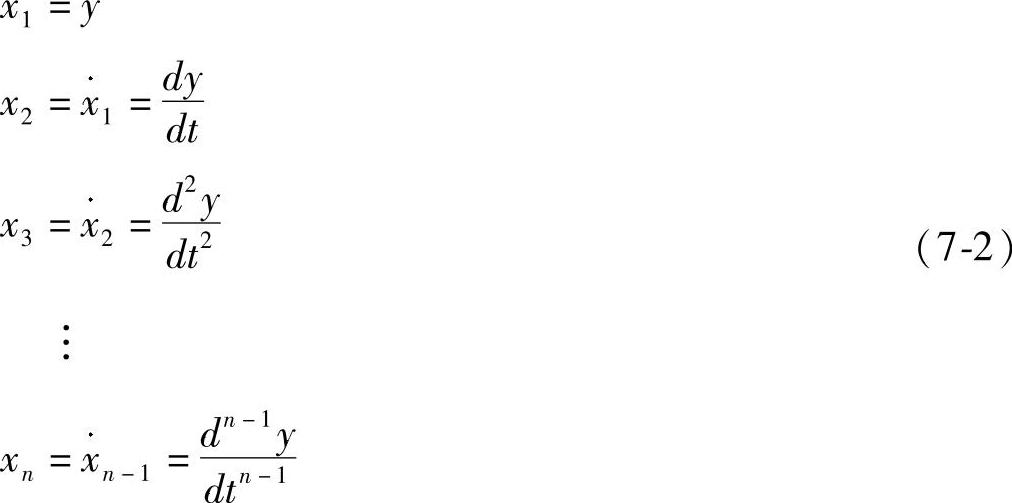
则有

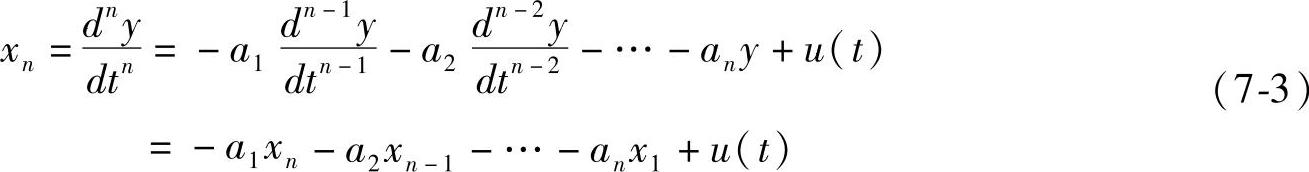
将上述n个一阶微分方程写成矩阵形式

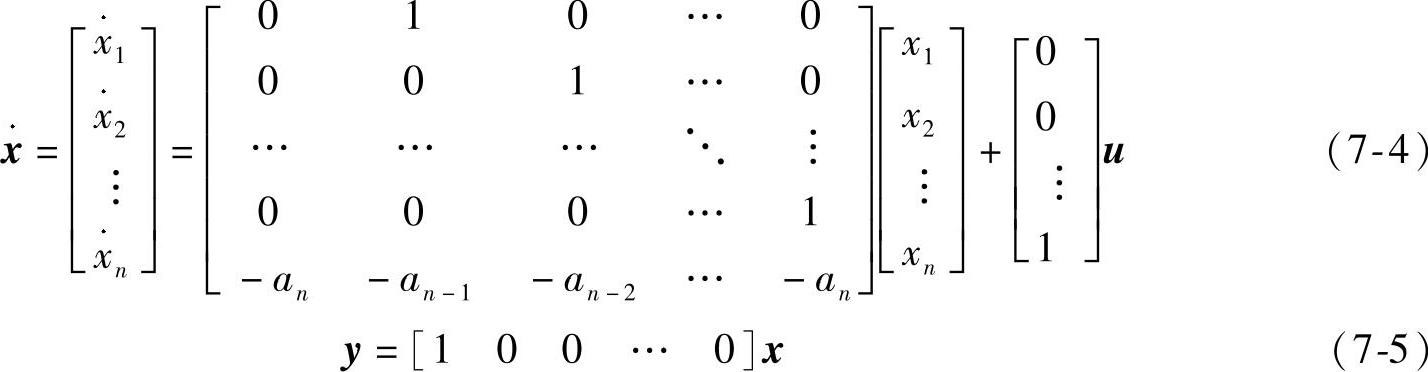
将公式（7-4）和（7-5）用图形表达出来，就是如图7-4所示的仿真模型。

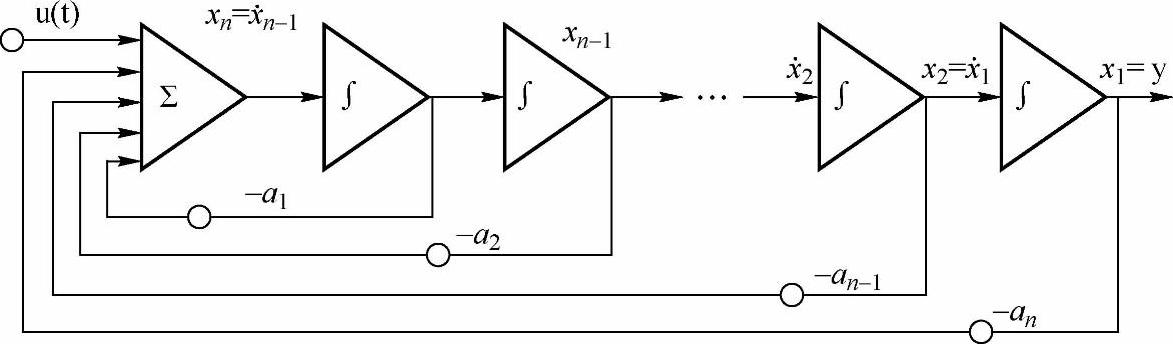
图7-4 仿真模型

若系统的微分方程如（7-6）式所示

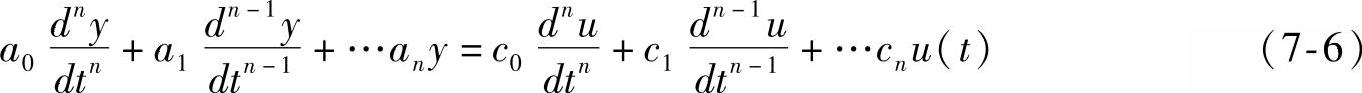(https://www.daowen.com)

系统初始条件为：y^（i）（t₀）=y₀^（i），u^（i）（t₀）=u₀^（i），（i=1，2，…，n-1）。

即方程右端不仅有u（t），还有u（t）的各阶导数及其初值，则上述方法难以直接使用。其仿真工作可以按照下面思路来进行。

先把方程（7-6）转换成n个一阶微分方程

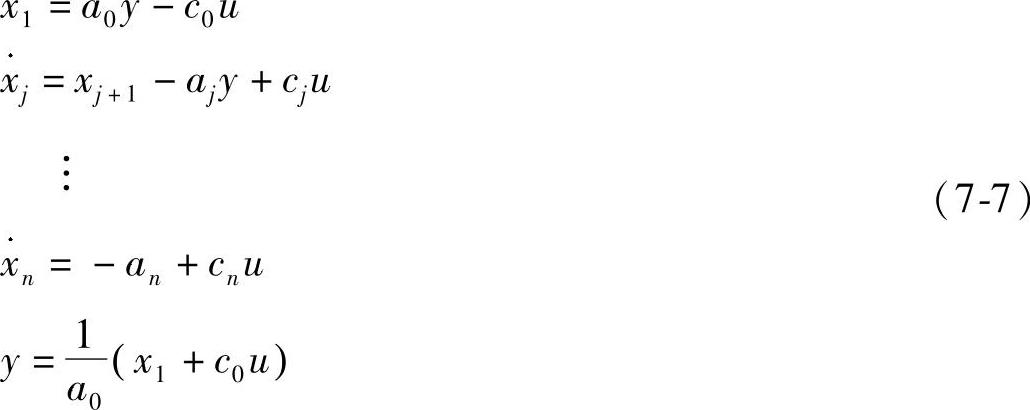
方程（7-7）与方程（7-6）等价，前者称为后者的伴随方程。

伴随方程以显式方式表达了状态变量与系统原输入/输出变量及其导数之间的关系，因而易于进行初始值转换。

接着求解以下系统状态方程及输出方程

其中

设a₀=1，初始值转换方程为