9.5.5 模糊综合评价的案例
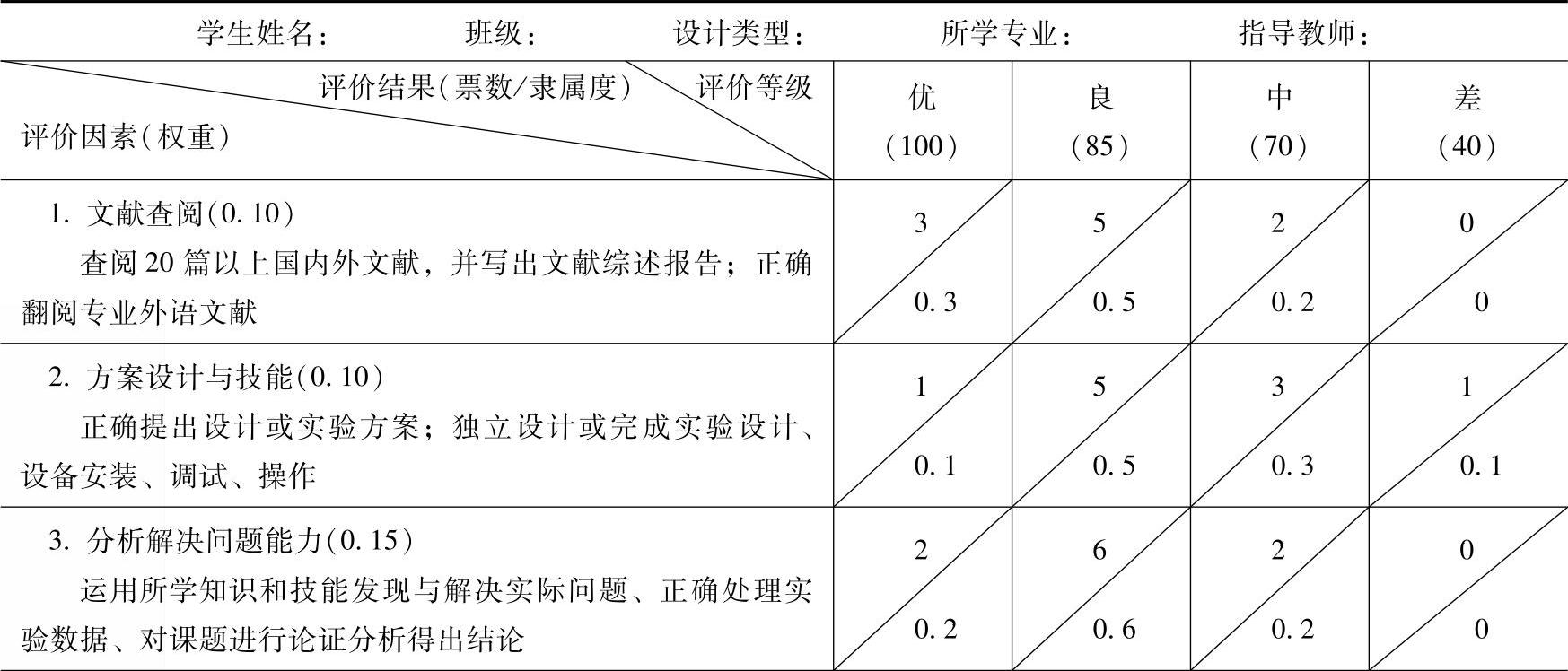
[案例1] 学生毕业设计答辩成绩的评定。表9-24是某理工大学学生毕业设计答辩评定表格。现在有一个学生参加毕业答辩,该答辩评审小组由10位教师组成。答辩小组组长要求每位教师依照答辩表格对这位学生答辩的表现和论文,从九个评价项目方面进行打分。答辩秘书随后收集10张表格,统计结果也见表9-24。现在要求依据模糊综合评价方法,计算该学生的答辩成绩。
解:依据题意,评价集V=[优/100,良/85,中/70,差/40]
9个评价因素的评价矩阵
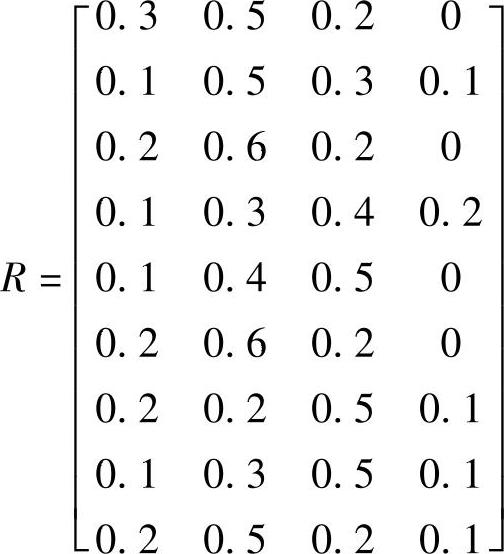
而各评价因素不同的权重
A={a1,a2,…,am}=[0.100.100.150.100.100.100.100.050.20]
运算矩阵的乘积
B=AR
得到
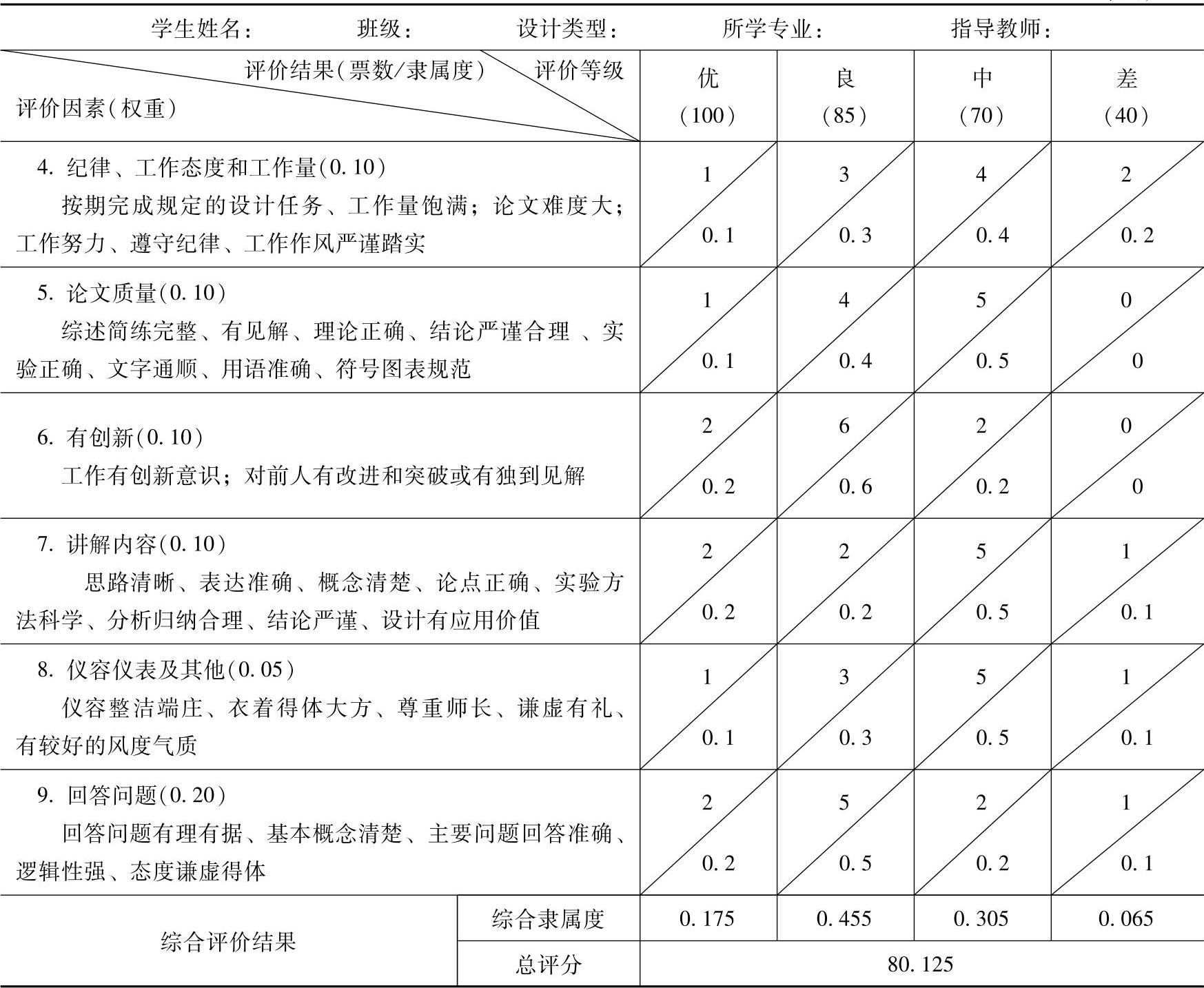
B=[0.1750.4550.3050.065]
最后再由B.VT运算,得到该同学答辩分数为80.125,成绩是良。
表9-24 某大学学生毕业设计答辩评定表格
(续)
[案例2] 某市科委收到各企业申报的科研课题6个。由于科研经费有限,不能全部拨款进行研究。为此,该部门请了十位有关专家,对这六个课题进行评议,以排出优先顺序供决策者进行拨款时参考。评审时专家们采用了模糊综合评判法进行了评议。
解:六个科研课题记为:S1、S2、S3、S4、S5和S6。
1)确定评价系统的评审因素集
U={u1u2u3u4 u5}式中,u1是立题必要性;u2是技术先进性;u3是实施可行性;u4是经济合理性;u5是社会效益性。
2)建立评价集:评价等级分为好、良、一般、差、较差五级
V=(0.90.70.50.30.1)
3)建立各评审要素的权重集
A=(0.150.200.100.250.30)
4)计算各评价系统的模糊综合评判矩阵。首先,根据上述评价项目及权系数、评价等级,十位专家对这六个课题S1、S2、S3、S4、S5和S6分别进行评议。评议结果见表9-25至表-30。
表9-25 第一个课题S1评议结果
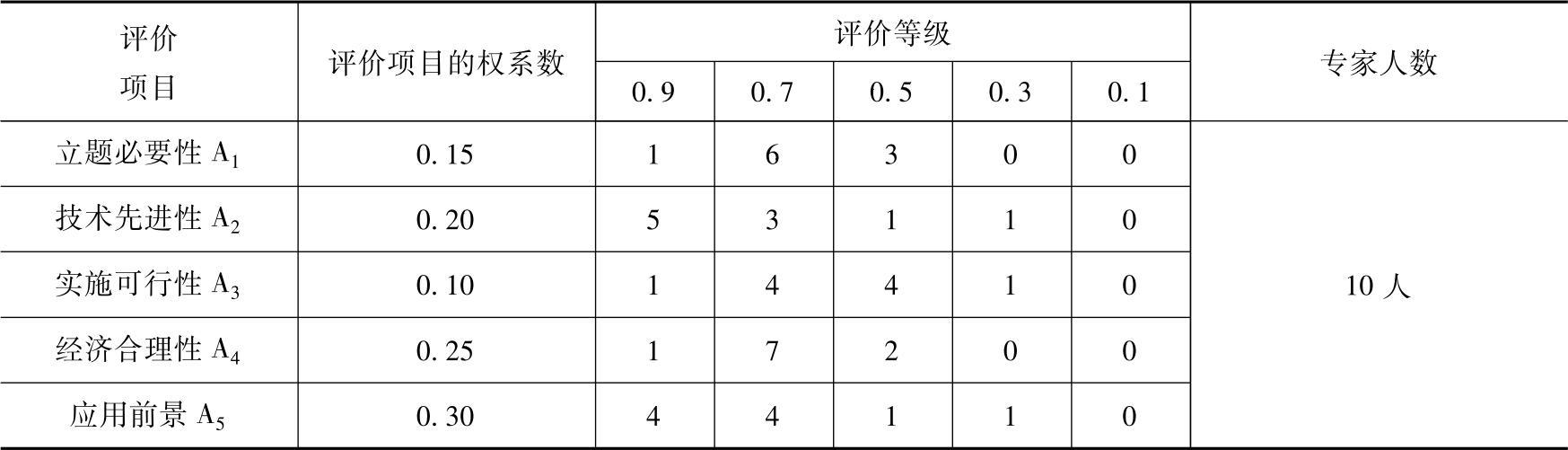
表9-26 第二个课题S2评议结果
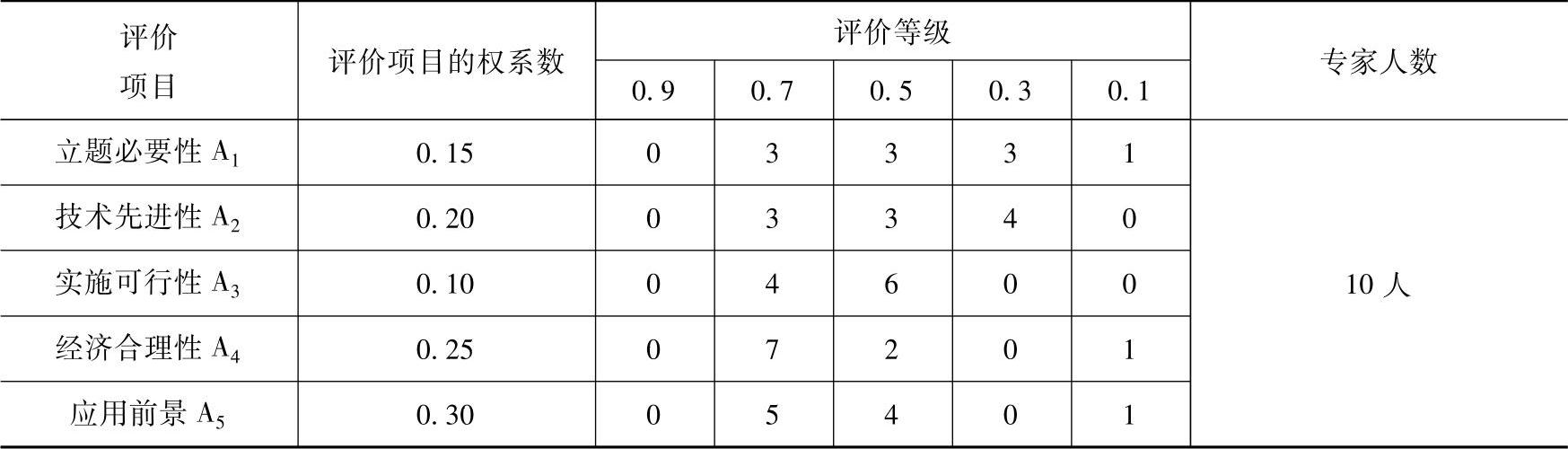
表9-27 第三个课题S3评议结果
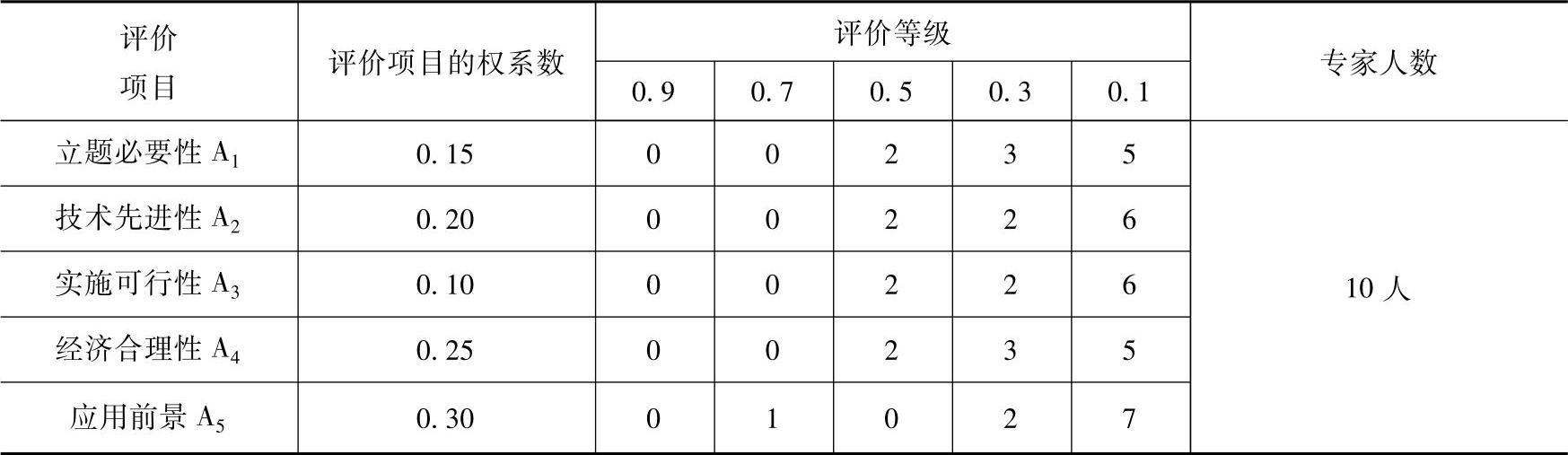
表9-28 第四个课题S4评议结果
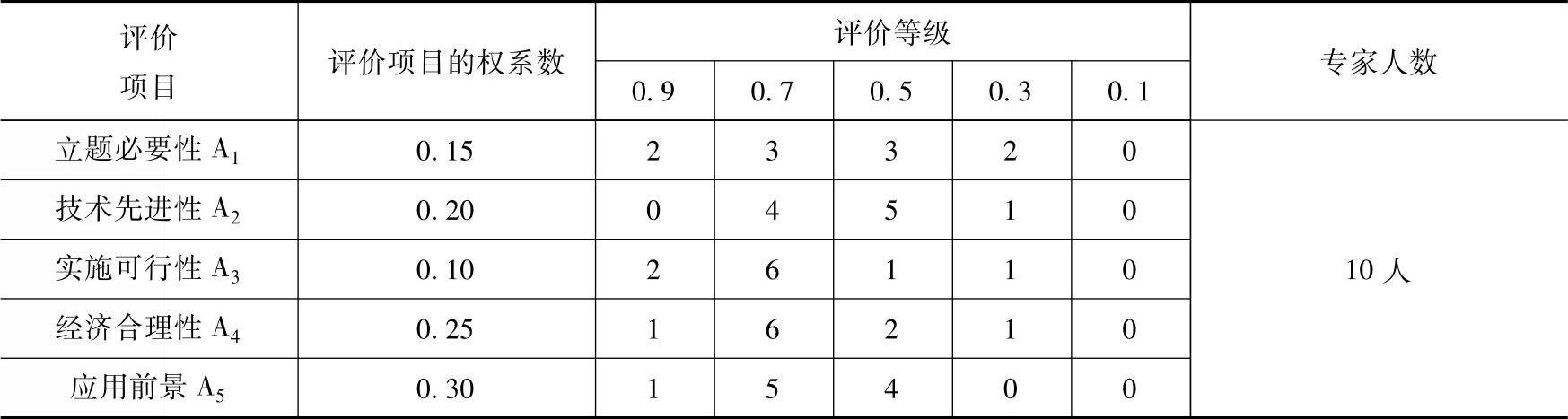
表9-29 第五个课题S5评议结果
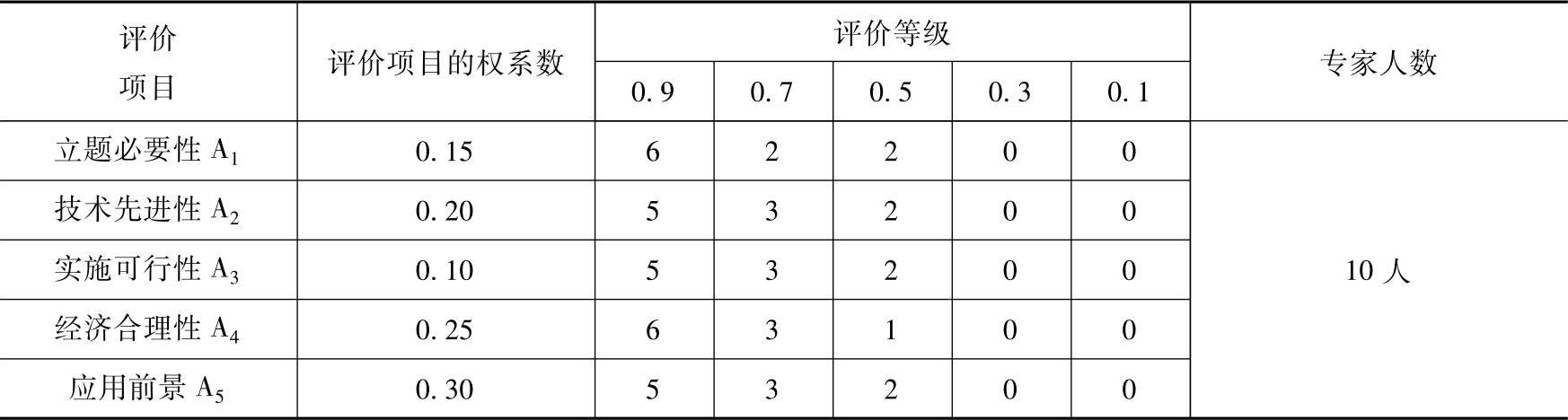
表9-30 第六个课题S6评议结果
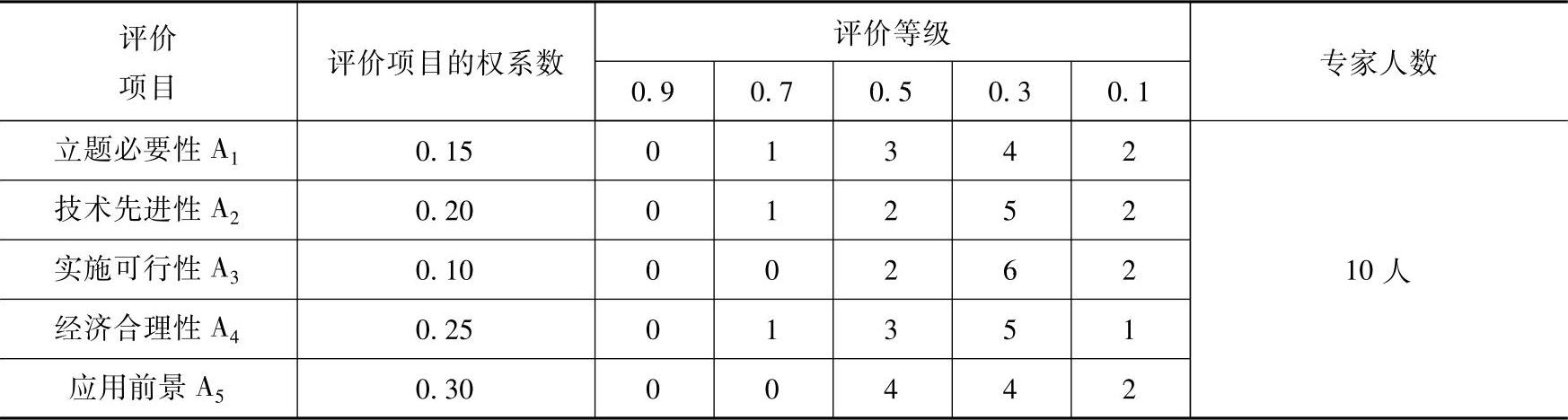
计算模糊综合评判矩阵
R=(rij)
式中,rij=dij/∑dij,dij是矩阵D=(dij)中的元素(https://www.daowen.com)
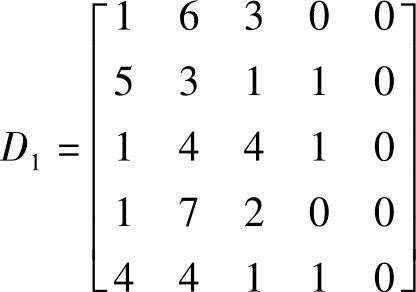
则
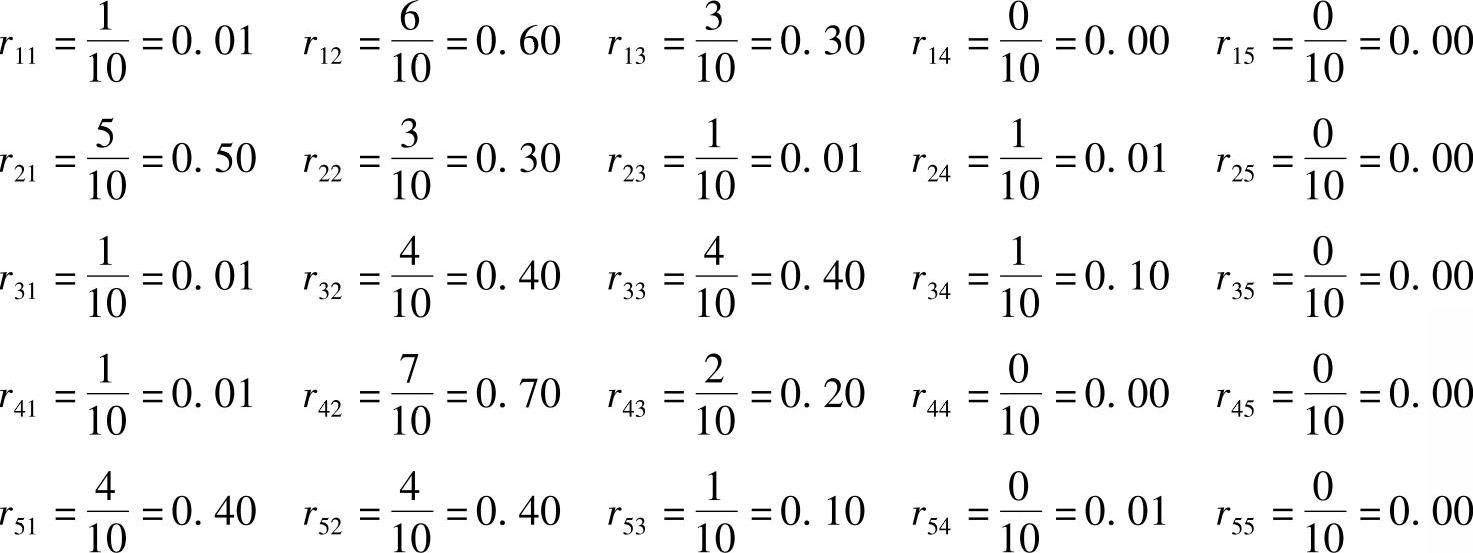
模糊综合评判矩阵
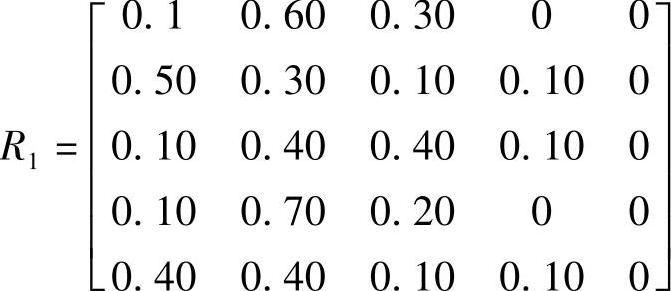
5)对模糊综合评判矩阵进行加权,得出模糊综合评价结果
Bi=A×Ri

6)计算各课题的评价等级
Ni=BiVT

依照上面方法,可以依次求出其他几个课题的评价等级
N2=0.541,N3=0.222,N4=0.622,N5=0.773,N6=0.349
7)比较各课题的评价值
0.773>0.693>0.622>0.541>0.349>0.222
因此,六个课题的优先排序:S5,S1,S4,S2,S6,S3。
[案例3] 某物流企业计划从同类重型载货汽车A、B、C、D中选择一种,主要从载货汽车的可靠性、动力性、安全性、节能环保、维修性、价格、售后服务和人机工程学8个方面来考虑。为此,聘请了十名专家讨论制定了评审要素集合、评价的权系数向量、评价等级等,对这四种载货汽车进行了模糊综合评价。评价过程如下:
1)确定系统评审要素集合为
U={动力性、可靠性、安全性、节能环保、维修性、价格、售后服务、人机工程学}
2)确定各评审要素的权系数行向量
P={P1,P2,P3,P4,P5,P6,P7,P8}
={0.55,0.20,0.1,0.05,0.05,0.03,0.01,0.01}
3)确定评价基准及相应的价值量
评价基准分为5个等级E={很好,较好,一般,较差,极差}
={e1,e2,e3,e4,e5}
相应的价值量为E={e1,e2,e3,e4,e5}={5,4,3,2,1}
4)对四种载货汽车计算关于各评审要素的模糊综合评判矩阵如下

5)对模糊综合评判矩阵进行加权,得出模糊综合评价结果
SA=PRA=(0.208,0.032,0.122,0.083,0.555)
SB=PRB=(0.113,0.077,0.106,0.498,0.206)
SC=PRC=(0.553,0.125,0.122,0.050,0.150)
SD=PRD=(0.032,0.543,0.215,0.100,0.110)
6)计算各评价载货汽车购买的可行度
NA=SAET=2.255,NB=SBET=2.393,NC=SCET=3.881,ND=SDET=3.287
7)比较各评价载货汽车的购买可行度,按可行度的大小排出先后次序并作出选择。
从可行度的大小来看,可行度最大的是载货汽车C,故应选择载货汽车C,同时载货汽车D作为备选。
