4.4.2 结构模型解析法
结构模型解析法(interpretative structural modeling,ISM)是美国Bottele研究所华费尔特教授于1973年在分析复杂社会经济系统问题时提出的。该方法把复杂系统分解为若干子系统(要素),利用实践经验、知识、计算机的帮助,最终将系统构造成一个条理分明多级递阶的结构模型。
ISM建模得到的模型属于概念模型,它可以把模糊不清的思想或看法转化为直观的具有良好结构关系的模型。ISM方法应用广泛,特别适用变量众多、关系复杂而结构不清晰的系统分析,也可用于方案排序、区域环境规划、城市规划设计等方面。
4.4.2.1 图的矩阵表示法
(1)邻接矩阵 描述图中各节点两两关系。
邻接矩阵也称相邻矩阵,A的元素aij可以定义如下

对于如图4-4所示的有向连接图,其邻接矩阵为
S1S2S3S4S5S6

邻接矩阵有如下特性:
①矩阵A的元素全为零的行所对应的节点称作汇点,即只有有向边进入而没有有向边离开该节点。S1点即为汇点。
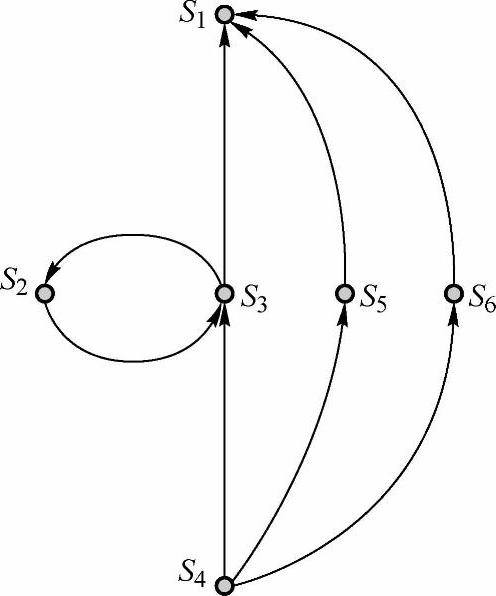
图4-4 有向连接图
②矩阵A的元素全为零的列所对应的节点称作源点,即只有有向边离开而没有有向边进入该节点。S4点即为源点。
③对应每一个节点的行中,其元素值为1的数量,就是离开该节点的有向边数目。
④对应每一个节点的列中,其元素值为1的数量,就是进入该节点的有向边数。
邻接矩阵描述了系统各要素两两之间的直接关系(从节点Si是否可以到达节点Sj)。
若在矩阵A中第i行第j列的元素aij=1,则表明节点Si与节点Sj有关系,也即表明从Si到Sj有一长度为1的通路,Si可以直接到达Sj。邻接矩阵描述了经过长度为1的通路后各节点两两之间的可达程度。
(2)可达矩阵 是指用矩阵形式来描述有向连接图各点之间,经过一定长度的通路后可以到达的程度。它反映了节点间直接、间接的连接关系。
可达矩阵M有一个重要特性,即推移律特性。
①当Si经过长度为1的通路直接到达SK,而SK经过长度为1的通路直接到达Sj,那么,Si经过长度为2的通路必可到达Sj。
②可达矩阵可以应用邻接矩阵A加上单位矩阵I,计算Ak=(A+I)k,并经过布尔演算(0+0=0;1+0=1;1+1=1;0×0=0;1×0=0;1×1=1)后求得。
③一般地,通过依次运算后可得
A1≠A2≠…≠Ar-1=Ar,r<=n-1 (4-11)
式中,n是矩阵阶数。则
Ar-1=(A+I)r-1=M (4-12)
矩阵M就称为可达矩阵,表明各节点经过长度不大于(n-1)通路可以达到的程度。可以证明,对于节点数为n的图,最长通路长度不超过(n-1)。
4.4.2.2 ISM的工作程序或步骤
1)组织实施ISM的小组。小组成员中,应包含持不同观点的人,还应包括能及时作出决策的负责人参加。
2)问题的设定或提出。
3)选择构成系统的要素及要素的集合。
4)根据要素明细表作构思模型,并建立邻接矩阵和可达矩阵。
5)对可达矩阵进行分解后建立结构分析模型。
6)根据结构分析模型建立系统层次结构模型。
[举例]现有如图4-5所示由7个节点组成的系统,试用结构模型解析法建立它的结构模型。
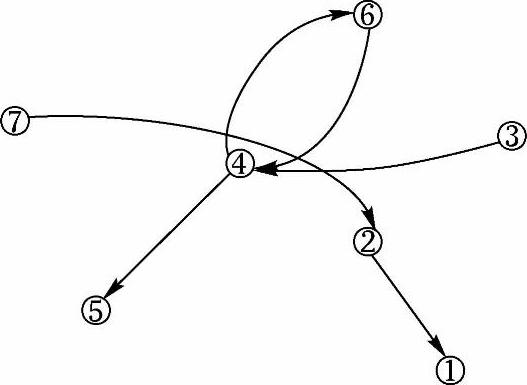
图4-5 有向连接图
解:根据分析,其关联矩阵可写为
S1S2S3S4S5S6S7

由于(A+I)≠(A+I)2=(A+I)3,所以可达矩阵M=(A+I)2,且
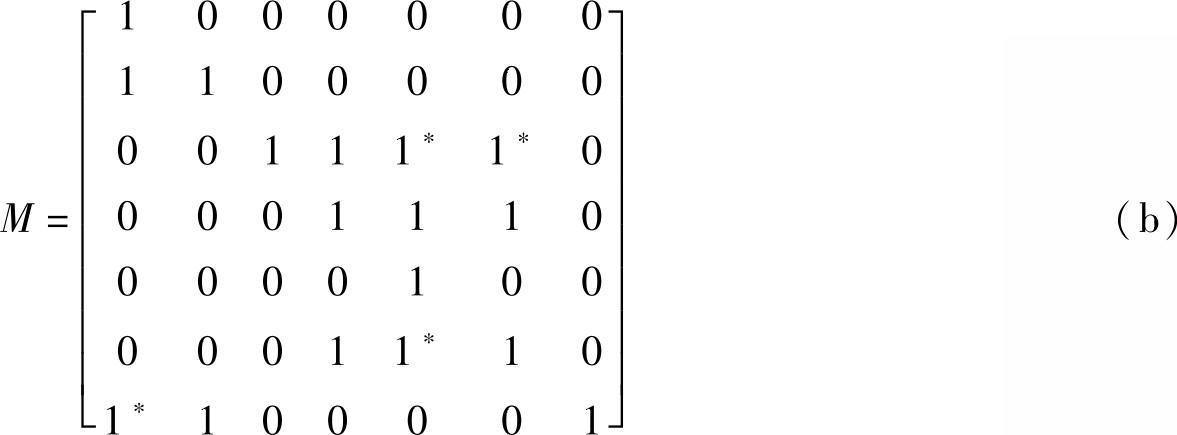
矩阵M中带“*”号的元素是原直接关系矩阵中所没有的,它反映出了系统节点之间的间接关系。M矩阵中主对角元素的1表示各节点的自联接。下一步利用上面获得的可达矩阵迸行系统结构的层次分析。
定义R(ni)为要素ni可达集合(简称可达集)
R(ni)={nj∈N|mij=1} (c)
R(ni)定义为由可达矩阵第ni行所有元素为1的列所对应要素集合。其中,N为所有节点集合;mij为i节点到j节点关联(可达)值,mij=1表示i关联j。R(ni)表示为要素ni上位集合。通俗地讲,由要素ni出发,可以直接和间接达到要素的集合(包括要素ni自已)就是上位集合R(ni)。在本案例中,可达矩阵M中,可达集R(n1)={1},R(n2)={1,2}。
将达到要素ni要素集合定义为要素ni先行集,用A(ni)表示(https://www.daowen.com)
A(ni)={nj∈N|mji=1} (d)
A(ni)定义为由矩阵中第ni列所有元素为1行所对应要素集合。且A(ni)表示为要素ni下位集合。通俗地讲,所有可以直接和间接达到要素ni要素的集合(包括要素ni自已)就是下位集合A(ni)。在本案例中,下位集A(n1)={1,2,7},A(n2)={2,7}。
把所有ni可达集合R(ni)与先行集合A(ni)交集等于先行集合A(ni)的要素集合定义为共同集合,用T表示:
T={ni∈N |R(ni)∩A(ni)=A(ni)} (e)
在本例中,R(1)={2,3,…,n,n+1,n+2},A(1)={2}
所以
T={ni∈N|R(1)∩A(1)=A(1)}={2} (f)
下面迸行区域划分、级间划分和强连通块划分。
1.区域划分
就是把要素之间关系分为可达与不可达,并巨判断哪些要素是连通的,即把系统分为有关系的几个部分或子部分。
首先,根据可达矩阵得到各个要素的R(ni)与A(ni),并计算R(ni)∩A(ni)。计算过程见表4-3。
表4-3 计算过程
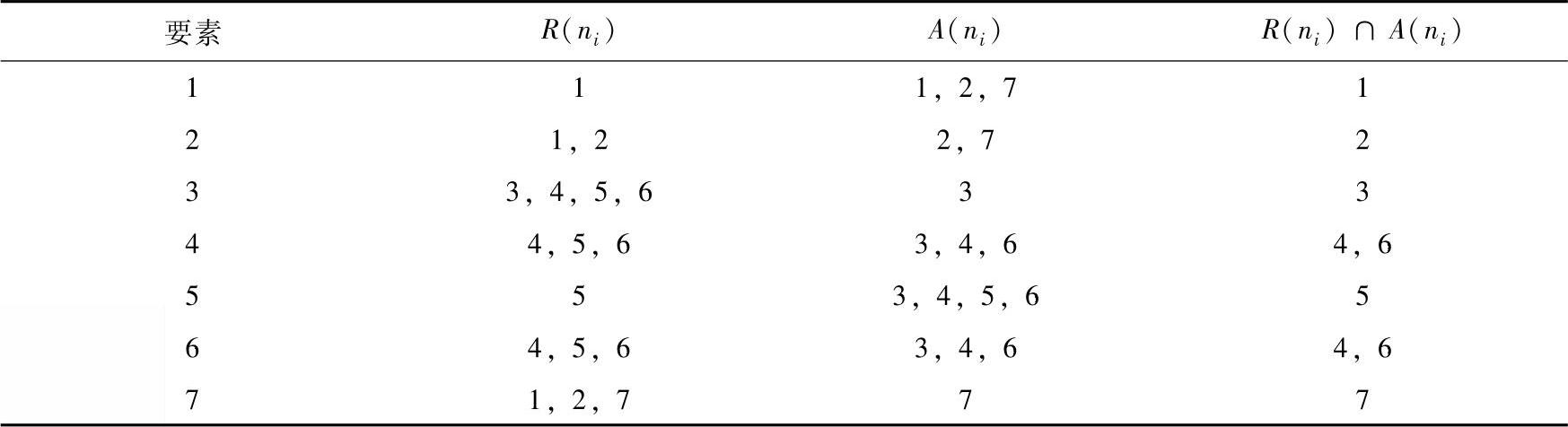
接着,利用计算公式:R(ni)∩A(ni)=A(ni)求出共同集合T
T={3,7},即求出底层要素的集合。
然后,可从这些要素3和7考虑起,找出与它们在同一部分中的要素。如果两要素ni、nj在同一部分内,则它们可达集有共同单元,即
R(ni)∩R(nj)≠φ(g)
否则,它们分别属于两个连通域。
在本例中,T={3,7}且R(3)∩R(7)=φ,则系统可以分为两个连通域:{1,2,7},{3,4,5,6}。
2.级间划分
级间(或层次)划分就是将系统中的所有要素,以可达矩阵为准则,划分成不同级(层)次。
由要素可达集和先行集定义,可以得到这样一个事实:一个多级结构,它最上级的要素ni可达集R(ni),只能由ni本身和ni强连接要素组成。两要素的强连接是指这两个要素互为可达的,在有向连接图中表现为都有箭线指向对方。具有强连接性的要素称为强连接要素。最高级要素ni先行集只能由ni本身和结构下一阶可能达到ni要素以及ni强连接元素构成。
如果ni是最上一级单元,它必须满足下述条件
R(ni)=R(ni)∩A(ni) (h)
可利用以上条件确定出结构最高级要素。
找出最高级要素后,即可将其从可达矩阵中划去相应的行与列;接着,再从剩下的可达矩阵中寻找新的最高级要素;依此类推,就可以找出各级所包含的最高级要素集合。
若用L1,L2,…,Lk表示从上到下的级次,则有k个级次的系统,级间划分可以用下式来表示
πk(n)=[L1,L2,…,Lk] (i)
若定义第0级为空级,即L0=∅。
3.强连通块划分
在进行级间划分后,每级要素中可能有强连接要素。在同一区域内同级要素中相互可达的要素就称为强连通块。
由表4-3可知:n1、n5满足R(ni)=R(ni)∩A(ni),故n1、n5分别为连通域中的最高级要素。因而L1={1,5}
去掉L1后,进行第二级划分,得到表4-4。
表4-4 第二级划分
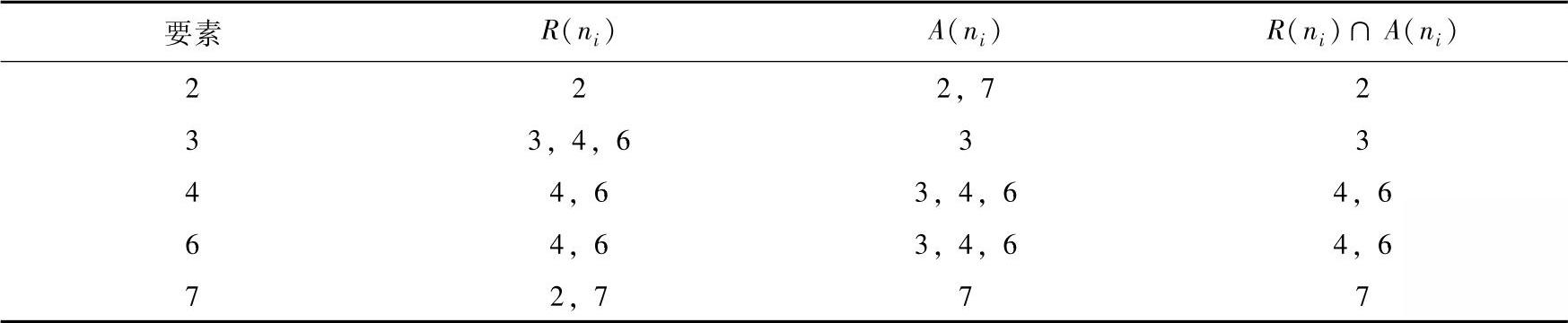
在表4-4中,n2、n4、n6满足R(ni)=R(ni)∩A(ni),故n2、n4、n6分别为连通域中第二级要素。巨L2={2,4,6}。
再去掉L2后,进行第三级划分,得到表4-5。
表4-5 第三级划分

所以L3={3,7}。也即系统结构最低阶元素有2个:3和7。
4.作出递阶有向图
结果如图4-6所示。
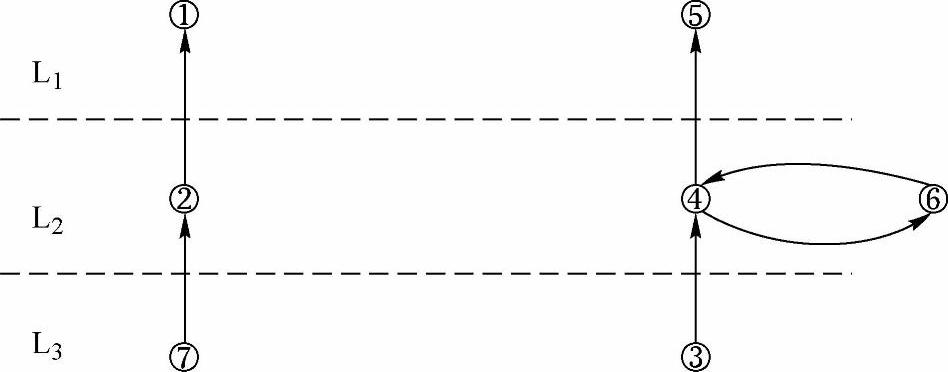
图4-6 递级层次给构
4.4.2.3 分析、讨论
对于一般工程系统,系统的邻接矩阵不难得到。对于社会经济系统,可达矩阵容易得到,因为根据人们的实践经验和直觉判断,比较容易知道要素间有无关系,至于这种关系是直接的还是间接的,则不需十分清楚。在这种情况下,可以通过对话形式先构成可达矩阵,再经过简化和排序等处理后即可得到结构模型。然后在结构模型的要素上,填入相应的要素名称,即为结构模型。
