10.4.2 决策准则
1.悲观准则(极大极小决策标准)
悲观准则又称极大极小决策标准。当决策者对决策问题不明确时,唯恐由于决策失误可能带来损失。因而,在做决策时,小心谨慎,总是抱着悲观的态度,从坏处着想,并从最坏的结果中争取最好的结果。
(1)决策步骤
1)编制决策益损表。
2)从每一个方案中选择一个最小的收益值。
3)在这些最小的收益值对应的决策方案中,选择一个收益值最大的方案为备选方案。
(2)决策原则 小中取大。由于这种决策标准是由Wald提出的,故又称“瓦尔特法”。
[案例1] 某物流公司需贷款组建一个车队,初步考虑了三个组建车队的方案:①组建大型车队;②组建中型车队;③组建小型车队。由于对业务量的多少不能确定,对不同规模的车队,其获利情况、支付贷款利息及营运费的情况都不同。经初步估算,编制出每个方案在每种不同的业务量下的益损值见表10-12。
表10-12 益损值表
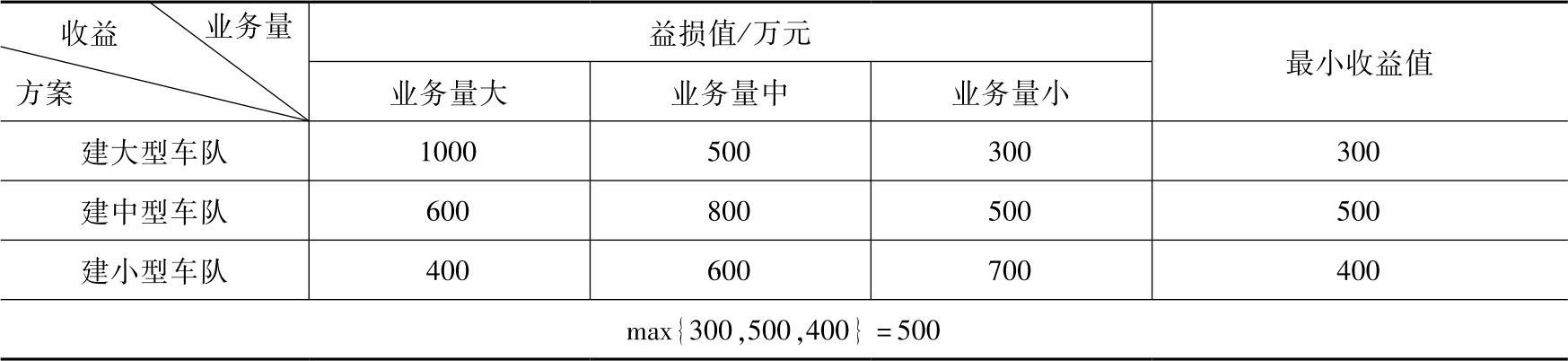
由表10-12可知,根据悲观准则,最优决策为组建中型车队,收益为500万元。
2.乐观准则
乐观准则又称极大极大决策标准。该标准与极大极小决策标准相反,它的主要特征是:实现方案选择的乐观原则。在进行决策时,决策者不放弃任何一个获得好结果的机会,争取大中取大,充满乐观冒险精神。
(1)决策步骤
1)编制决策益损表。
2)从每一个方案中选择一个最大的收益值。
3)在这些最大的收益值对应的决策方案中,选择一个收益值最大的方案为备选方案。
(2)决策原则 大中取大。
[案例2] 用乐观准则求[案例1]的最优决策方案。
计算结果见表10-13。
表10-13 最大收益值表
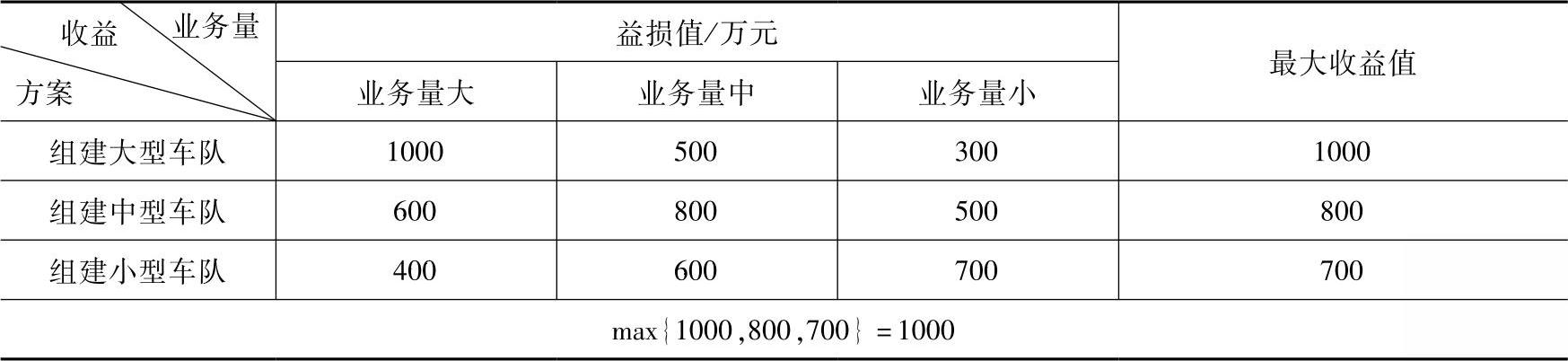
由表10-13可知,根据乐观准则,采用组建大型车队方案,收益为1000万元。
3.折中准则
折中决策标准是介于乐观决策标准和悲观决策标准之间的一个决策标准。在进行决策的时候,要求决策者确定一个系数:折中系数α,巨0<α<1。
决策步骤如下:
1)编制决策益损表。
2)计算每个方案的折中决策标准收益值=αOmax+(1-α)Omin
其中:Omax——同一方案的最大收益值;Omin——同一方案的最小收益值。
3)选择最大的折中收益值对应的方案为备选方案。
说明:当α=1时,为乐观(极大极大)准则;当α=0时,为悲观(极大极小)准则。
[案例3] 用折中决策标准求[案例1]的最优决策方案,取折中系数为α=0.7。计算结果见表10-14。(https://www.daowen.com)
表10-14 收益值表
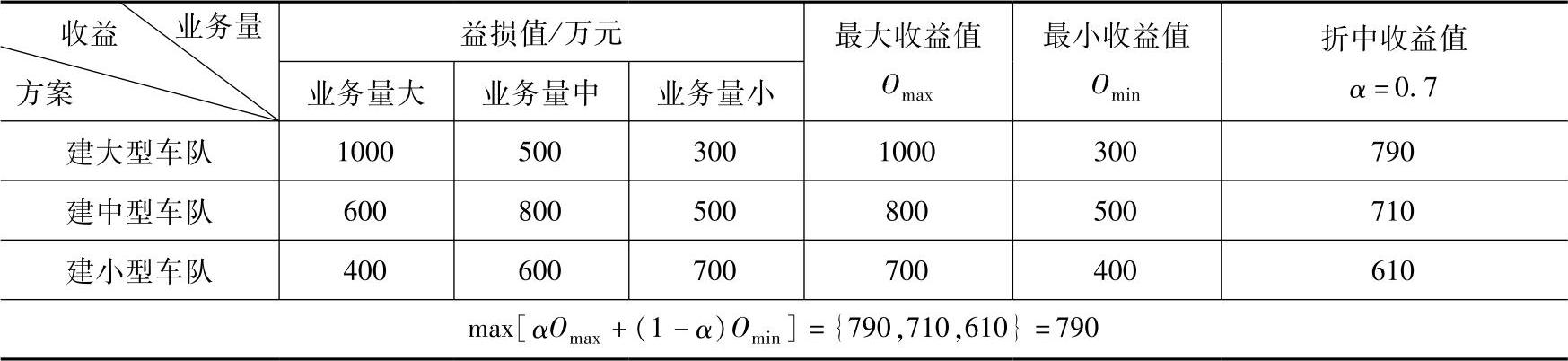
由表10-14可知,根据折中准则,选择组建大型车队的方案,折中收益为790万元。
4.等可能性准则
特点:在对未来事件发生概率缺乏了解情况下,没有理由认为哪一种自然状态出现可能性大些或小些,认为每种自然状态出现概率相同。此时决策转化成风险性决策,再采用风险性决策中的期望值准则,就可以得到最优决策。
[案例4] 用等可能性标准求[案例1]的最优决策方案。计算结果见表10-15。
表10-15 益损值表
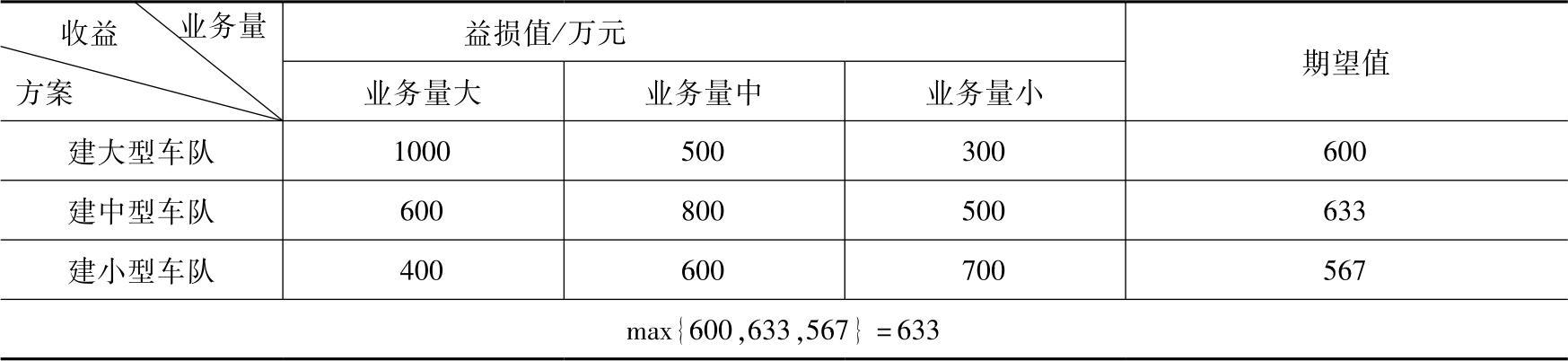
由表10-15可知,根据等可能性准则,选择组建中型车队方案,收益值为633万元。
5.后悔值准则
在决策过程中,当某一种自然状态可能出现时,决策者必然首先要选择收益最大的方案。如果决策者由于决策失误未选取这一方案,而是选择了其他方案,就会感到遗憾和后悔。这样两个方案的收益值之差就叫做遗憾值或后悔值。遗憾值标准就是为避免将来后悔而设计的一种决策方法。
利用该准则的决策步骤如下:
1)编制决策益损表。
2)用每个状态下的最大收益值减去其他方案的收益值,得出每个方案的遗憾值。
3)找出每个方案的最大遗憾值。
4)从每个方案的最大遗憾值中找出最小的遗憾值对应的方案为备选方案。
[案例5]用遗憾值准则求[案例1]的最优决策方案。
解:
1)从决策收益表中用“*”号标出不同状态下的最大收益值,见表10-16。
2)用每列带有“*”的最大收益值减去各个方案的收益值,列出遗憾值表,见表10-16。
3)从表10-16每个方案的遗憾值中找出最大的遗憾值,得到表10-17中最后一列的数字。
4)从每个方案的最大遗憾值中选出最小的遗憾值对应的方案为备选方案。
表10-16 益损值表

表10-17 遗憾值表
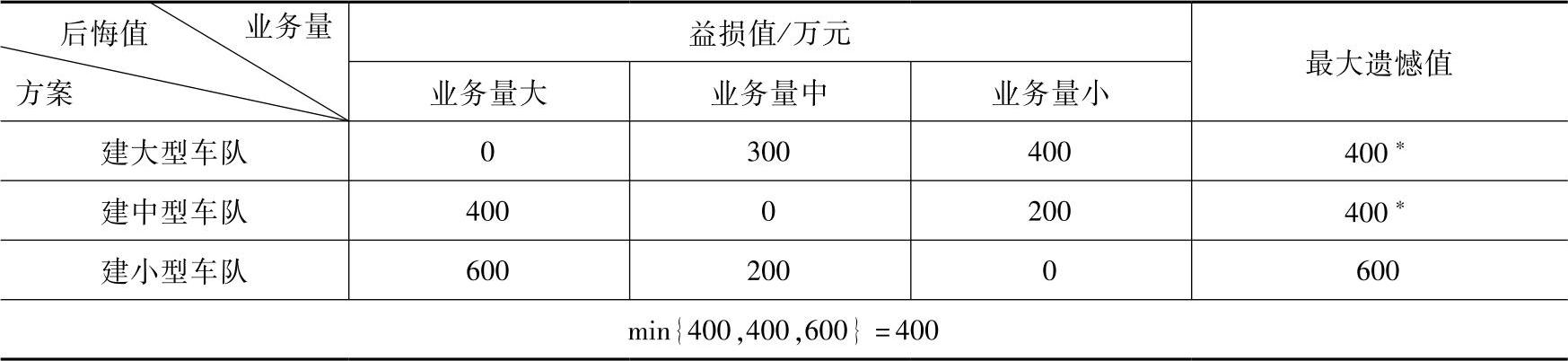
根据遗憾值准则,此时有两个方案可供选择:选择组建大型车队方案或选择组建中型车队方案,后悔值均为400万元。
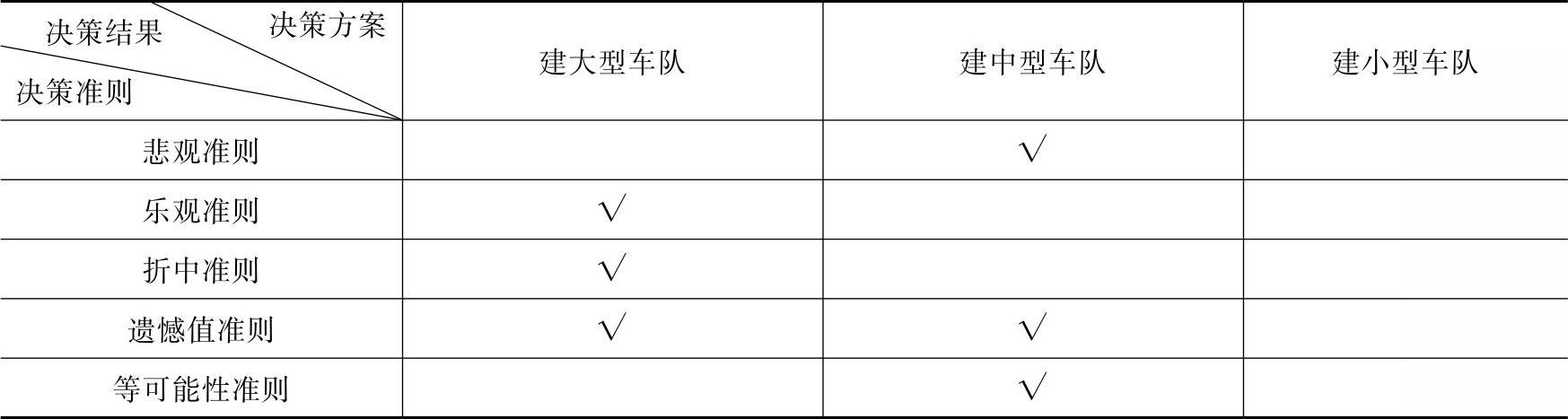
上面讨论了不确定情况下的五种决策标准,具体进行决策时,可以将几个标准同时使用,将选中次数最多的方案作为备选方案。如在前面几个例子中,5个决策标准的决策结果见表10-18。最后结论:选择组建大型车队或中型车队方案。
表10-18 五种准则的决策结果