8.3.2 工作(或工序)的时间参数
工作(或工序)的时间参数有6个,分别为:工序最早开始时间tES(i,j);工序最早结束时间tEF(i,j);工序最迟开始时间tLS(i,j);工序最迟结束时间tLF(i,j);工序的总时差Δt(i,j);工序的单时差或分时差ΔtF(i,j)。
1.工序最早开始时间tES(i,j)
工序最早开始时间指的是一个工序的紧前工序全部完工,本工序可能开始的最早时刻。计算方法是用该工序的紧前工序的最早开始时间,加上紧前工序的工时,当遇到紧前工序有多个时,应选其中最早开始时间加上该项工序之和的最大值。规定与始点事项相连接的各个工序的最早开始时间等于零。计算时应从与始点事项相连接的工序开始,自左到右,依次计算。以上过程,用数学公式表示为
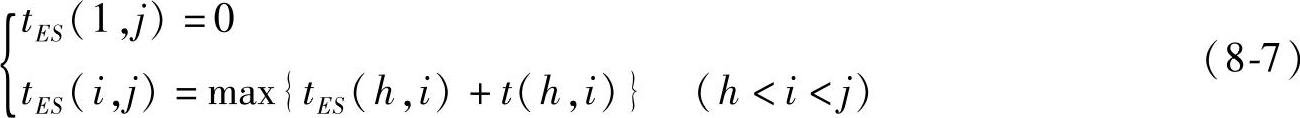
某项工序的最早开始时间,数值上与该工序箭尾事项的最早开始时间相等,即(https://www.daowen.com)
tES(i,j)=tE(i) (8-8)
将工序的最早开始时间的计算结果,填入相应工序上(下)方的第一个方格中。
2.工序最早结束时间tEF(i,j)
某项工序的最早结束时间是指一个工序必须等它紧前各工序完工后,其自身也完工的时间。用公式表示为
tEF(i,j)=tES(i,j)+t(i,j) (8-9)
具体计算时,把箭线上(下)方第一个方格中的数,加上所在箭线上的工序时间,其结果填入第二个方格中。
与终点相连工序的最早结束时间为总工期,当有多个工序与终点相连时,总工期为各工序最早结束时间的最大值,用公式表示为
总工期=max{tEF(i,n)} (8-10)
3.工序最迟开始时间tLS(i,j)
某项工序的最迟开始时间是指在不影响其紧后各工序按时开始,该工序最迟必须开始的时间值。计算方法是用该工序的紧后工序的最迟开始时间,减去本身的工时。当遇到紧后工序有多个时,应选其中紧后各工序最迟开始时间分别减去该工序工时之差的最小值。与终点相连接的各工序的最迟开始时间,等于总工期减去各自的工时。
工序的最迟开始时间的计算方向是从与终点相连的工序开始,由右到左,以此计算。以上过程用公式表示为
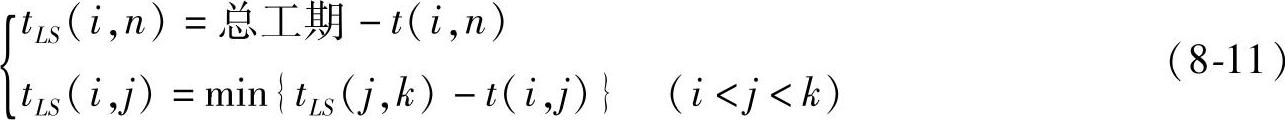
某项工序的最迟开始时间,数值上也等于该工序箭头事项最迟结束时间减去自身工时之差,即
tLS(i,j)=tL(j)-t(i,j) (8-12)
将工序的最迟开始时间的计算结果,填入相应工序上(下)方的第三个方格中。
4.工序最迟结束时间tLF(i,j)
某项工序的最迟结束时间是指在不影响其紧后各工序按时开工,该工序最迟完工时间。计算方法是用该工序的最迟开始时间,加上本身的工时,即
tLF(i,j)=tLS(i,j)+t(i,j) (8-13)
将工序的最迟结束时间的计算结果,填入相应工序上(下)方的第四个方格中。
某项工序的最迟结束时间,数值上也等于该工序箭头事项最迟结束时间,即
tLF(i,j)=tL(j) (8-14)
5.总时差Δt(i,j)
某项工序的总时差是指该工序的完工期,在不影响整个项目总工期的条件下,可以推迟的机动时间。总时差的时间值等于该工序的最迟开始时间减去最早开始时间,或该工序的最迟结束时间减去最早结束时间。某工序的总时差,数值上也等于该工序箭头事项的最迟结束时间,减去箭尾事项的最早开始时间,再减去工时。以上过程用公式表示为
Δt(i,j)=tLS(i,j)-tES(i,j)=tLF(i,j)-tEF(i,j)=tL(j)-tE(i)-t(i,j) (8-15)
总时差的计算结果用方括号括起,标在相应工序箭线的下方。在网络图中,总时差为零的工作为关键工作,而连接所有关键工作所形成的线路为关键线路。
下面分析总时差的意义。任取一个作业或工作(i,j)来分析。如果它在最早开始时间tES(i,j)开工,并巨耗费规定工时t(i,j),则它一定能在最早完成时间tEF(i,j)完工;但工作(i,j)又有一个最迟完成时间tLF(i,j),只要工作(i,j)不超过tLF(i,j)就完工,则不会拖延整个任务的工期。所以,作业的安排具有一定的回旋余地,其回旋范围就称为工作(i,j)的总时差。
当Δt(i,j)=0时,称工作(i,j)为关键工作。当Δt(i,j)≠0时,工作(i,j)可以作如下两种机动安排:或者适当推迟其开工时间(不超过其最迟开始时间),或者适当放慢进度、延长其工时t(i,j)(延长的幅度不超过Δt(i,j)就行)。当然,也可以将两种机动安排结合使用:即适当推迟一些开工时间,又适当放慢一些该工作的进度。这些情况称为时差的调用,即调用量为δ(i,j)。则调用原则可统一表示为δ(i,j)≤Δt(i,j)。
综上所述,Δt(i,j)的数值实际上表明工作(i,j)具有潜力,调用时差就是挖掘其中的潜力(人力、物力和财力)。
6.单时差或分时差ΔtF(i,j)
某项工序的单时差或分时差ΔtF(i,j)是指一个工序的完工期,在不影响紧后各工序最早开始的条件下,可以推迟的时间。ΔtF(i,j)的时间值等于该工序的紧后工序最早开始时间减去本工序的最早结束时间之差。计算结果用圆括号括起,标在相应箭线的下方。某工序的分时差,数值上也等于该工序箭头事项的最早开始时间,减去箭尾事项的最早开始时间,再减去工时。以上过程用数学公式表示为
ΔtF(i,j)=tES(j,k)-tEF(i,j)=tE(j)-tE(i)-t(i,j)(i<j<k) (8-16)
单时差是该工作所独有的,只能在本工作中加以利用,不能转让给其他工作使用。一项工作要利用时差,首先应利用单时差,不足时再考虑利用总时差中的其他部分。
当Δt(i,j)≠0而ΔtF(i,j)>0时,只要满足ΔtF(i,j)≤Δt(i,j),整个任务的总工期是不会拖延的。但是对于后续作业(j,k)来说,则会出现两种情况:一是后续作业受到干扰,无法在其最早开始时间tES(j,k)开工;二是后续作业不受干扰,仍然可以在tES(j,k)开始。对于后一种情况,我们称作业(i,j)具有“单时差”,记为ΔtF(i,j)。就是说,作业(i,j)的单时差ΔtF(i,j)定义为:在不影响后续作业(j,k)的最早开始时间tES(j,k)的前提下,作业(i,j)可以自由地利用机动时间的范围。
7.三种时差之间的关系
由于
Δt(i,j)=tL(j)-tE(i)-t(i,j),ΔtF(i,j)=tE(j)-tL(i)-t(i,j) (8-17)
Δt(i)=tL(i)-tE(i),Δt(j)=tL(j)-tE(j) (8-18)
所以
Δt(i,j)=Δt(i)+Δt(j)+ΔtF(i,j) (8-19)
由式(8-19)可知:工作的总时差等于它的箭尾事项与箭头事项的时差之和,再加上其本身的单时差。
以上是用公式计算的。用公式计算,步骤简单机械,不容易出错。也可以直接在图上进行计算,简单迅速,但在工序很多和网络图复杂的情况下,容易出错和遗漏,故用表格法进行计算比较合适。
