9.5.4 模糊综合评价法
1.模糊综合评价方法概述
对于方案、人才、成果的评价，人们的考虑往往是从多种因素出发的，而巨这些考虑一般只能用模糊语言来描述。例如，评价者从考虑问题的诸因素出发，参照有关的数据和情况，根据他们的判断对复杂问题分别作出“大、中、小”；“高、中、低”；“优、良、中、劣”；“好、较好、一般、较差、差”等程度的模糊评价。然后通过模糊数学提供的方法进行运算，就能得出定量的综合评价结果，从而为正确决策提供依据。
模糊理论着重研究“认知不确定”类问题，其研究对象具有内涵明确但外延不明的特点。模糊综合评价就是利用模糊集理论对某评价方案各指标的实现程度进行综合，凭经验借助隶属度函数，根据既定的标准得出综合性的评价。由于模糊方法更接近于东方人思维习惯和描述方法，因此它更适应于对社会经济系统及工程技术问题进行综合评价。
（1）模糊的概念及度量在日常生活中，东方人描述某人的身高时常用“高个子”或“低个子”等语言来描述，虽然描述中并未指明该人身高有多少厘米，但听众已大致了解该人的身高状况，并巨很容易依据这些模糊的特征来找到此人。这种描述的不确定性就是模糊性。为了定量地刻画这种模糊概念，常用隶属函数A来表述。如对身高而言，A=（1/180，0.5/1.75，0.2/170，0/165）表示身高180cm为高个子、175cm身高者为高个子的程度仅为0.5，依此类推。显然隶属度表征模糊性。
（2）模糊变量的运算 由于模糊变量是用隶属度描述的，因此其运算应为模糊运算。设有模糊矩阵
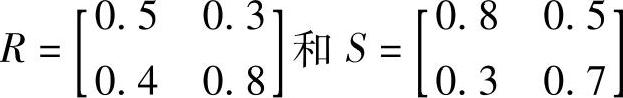
则R与S的并与交运算的规则与集合运算相似，并运算为两中取大，交运算为两中取小。
模糊矩阵的乘积定义如下
记C=R·S
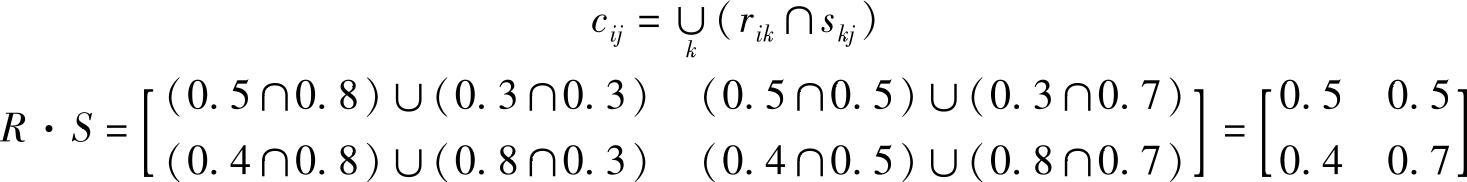
（3）模糊综合评价 设有一个评价问题：评判因素集U={u1，…un}，评价集V={v1，…vn}，各评价指标的权重分别为W1，W2，…，Wn，则综合评价问题可描述为计算模糊乘积U·V。对于此模糊乘积，也有学者提出取小取大运算（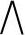
，
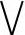），这样的折中运算往往会丢失大量信息达不到有意义的结果，所以建议把模糊乘积改成普通矩阵乘积，即
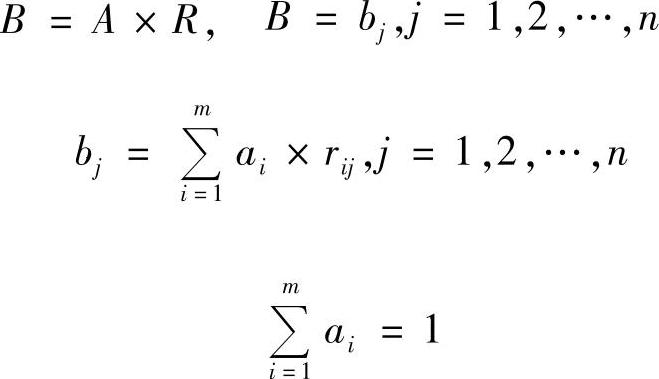
下面通过一个例子来说明。
[案例] 某服装厂对某一新产品进行评判，评判因素集U={款式色彩，穿着舒适，价格费用}，评价集V={很好，较好，不太好，不好}。并请若干专家与顾客进行评价。若对款式色彩有20%人很欢迎，70%人比较欢迎，10%的人不太欢迎，则可以得出对款式色彩评价的隶属度
A款式色彩={0.2/很欢迎，0.7/较欢迎，0.1/不太欢迎，0.0/不欢迎}
类似地，穿着舒适评价的隶属度有
A穿着舒适={0/很欢迎，0.4/较欢迎，0.5/不太欢迎，0.1/不欢迎}
价格费用评价的隶属度有
A价格费用={0.2/很合理，0.3/较合理，0.4/不太合理，0.1/不合理}
由以上可得模糊矩阵
如已知顾客考虑三个因素的权重为
a={0.2，0.5，0.3}
则顾客对该服装的综合评判为
b=a·R=（0.20.40.50.1）
即综合评价介于不太欢迎与较欢迎之间。其中不欢迎的比例要高一些。
如果把模糊运算改成普通矩阵运算，则顾客对该服装的综合评判为
b=a×R
=（0.2×0.2+0+0.3×0.20.2×0.7+0.5×0.4+0.3×0.30.2×0.1+0.5×0.5+
0.3×0.40.2×0.0+0.5×0.1+0.3×0.1）
=（0.10.430.390.08）
即综合评价介于较欢迎与不太欢迎之间，其中欢迎的比例要高一些。
（4）模糊综合评价方法解决问题的步骤
1）建立因素集
U={u1，u2，…，um}
式中，各元素ui（i=1，2，…，m）代表各影响因素。
2）建立评价集
V={v1，v2，…，vn}
式中，各元素vi（i=1，2，…，n）可以是非数量的，如语言形式{很欢迎，欢迎，一般，不欢迎}，及{优，良，中，劣}，{大，较大，中，小，较小}等；也可以是数量的，如一个部件的安全系数{1.5，2.0，2.5，3.0}。
3）建立权重集。为了反映各因素的重要程度，赋予各因素不同的权重
A={a1，a2，…，am}，且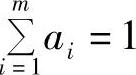
，ai≥0 i=1，2，…，m
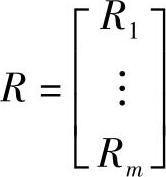
4）建立评价矩阵。单独从因素集U中一个因素ui（i=1，2，…，m）出发，对于评判对象进行评判，可以得到单因素评判集Ri（i=1，2，…，m）。综合评价集，得到评价矩阵R
5）进行模糊运算或逻辑数学运算，得到综合评判。单因素评判仅反映一个因素对评判对象的影响，而综合评价需要考虑各因素的影响，即需要完成以下模糊运算或逻辑数学运算，才能得到多因素指标的综合评判
B′=A·R或B′=A×R
如果给各评价级一个尺度
C=（1.0/优秀0.8/良好0.7/中0.4/差）
或C=（100/优秀80/良好70/中40/差）
或按照5个等分
C=（90/优秀70/良好50/一般30/差10/较差）
则
B=CB′T
B就是最后的评判结果。