7.2.2  仿真模型的最小实现

7.2.2 仿真模型的最小实现

一个系统有多种实现，因而仿真模型也不是唯一的。但必有一部分的系统矩阵A具有最小维数，也就是最小实现。对照图7-4可知，A的维数直接对应着仿真模型中的积分器的个数。如果从仿真模型的简单性和系统可观测性来看，显然希望采用系统的最小实现来作为仿真模型。

由给定的传递函数G（s）或脉冲响应函数H（s），建立与输入/输出特性等价的状态方程

C（SI-A）-1B=G（S） （7-10）

满足上式的（A、B、C）称为系统G（S）的实现。而所谓的最小实现就是要求传递函数G（S）具有最简单形式。最小实现的充分必要条件是（A、B、C）为完全能控，巨完全能观测。

例如有一线性系统，可用如下的微分方程来描述

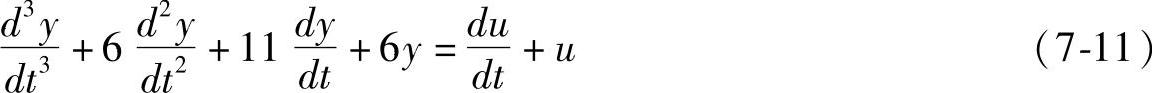
设y（t）和u（t）以及它们的各阶导数之初值均为零，则上式的传递函数可表达为

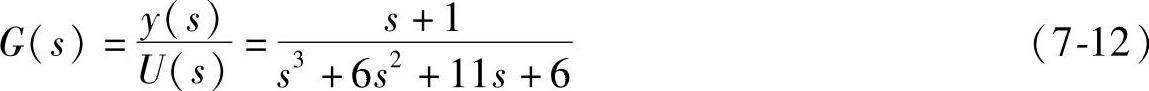
上式G（s）的最简单形式为

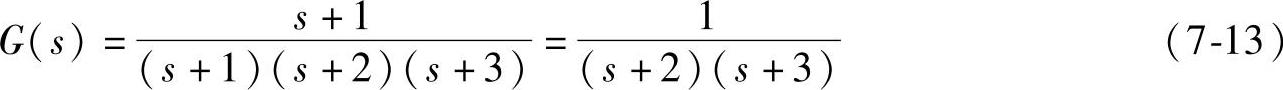
此时，系统的A、B、C分别为

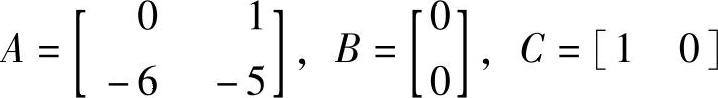
这个（A、B、C）是能控、能观测的，因此是最小实现。利用这个模型来仿真只需要两个积分器就可以。